92 (92)

182

W rozdziale tym zamieszczono wzory do obliczania sprężyn śrubowych walcowych przanoszęcych ąlły ściskające bądź rozciągające.

O wartości naprężeń w sprężynie śrubowej walcowej poddanej działaniu siły P (rys. 11.45) oraz o jej odkształceniu decyduje skręcanie drutu aprężyny, przy czym ramie momentu skręcającego dla każdego przekroju wynosi 0/2 1 w każdym przekroju występuje jednakowy moment skręcający

M₆-P§.    (li.13)

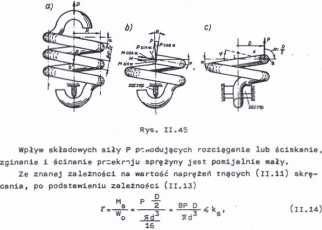
oblicza aię średnicę d przy znanym obciążeniu i wartości dopuszczalnego naprężania k dla danego materiału, z którego będzie wykonana sprężyna lub oblicza się siłę obciążającą sprężynę przy danych pozostałych parametrach.

Wyrażenie na skrócenie (wydłużenie) sprężyny    .

(11.15)

-'■T*

Wprowadzajęc pojęcie stałej sprężyny

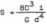
wzór (IX.15) zaplauje się w postaci

(11.17)

Do przejęcia dużych obclężeń przy ograniczonych wyalsrach obrysu stosuje się współosiowe układy sprę2yn.

Całkowite obciężenls układu wyraZa się wzorea

Pm £ P_±.    (II.18)

Stałę sprężyny oblicza eię z zależności    '

C - £Cj.    (II.19)

Podobnie dla sprężyn przy równoległym ustawieniu (zarówno dla sprężyn naciskowych Jak 1 nacięgowych)

(11.20)

(11.21)

II.3.1. Rurka o wymiarach d_z - 0,3 m, grubości ścianki g ■

•    2,5 • 10^-3 ■ 1 długości 1 • 0,8 a skręcana na całej długości momentem M_g - 14,25 Nm wykazała kęt skręcenia tp - 0,2° ■ 0,2 j§q *

•    0,00349 rad. Ta sama rurka rozclęgana siłę P - 1,75 • 10⁴ N wydłuży się o Al = 0.32 aa. Na podstawie tych prób wyznaczyć stałe dla zastosowanego materiału:

E - moduł sprężystości,

G - moduł sprężystości postaciowej,

V - liczbę Poissona.