CCF20101219004 (3)

Aksjomat 3. Nie naruszając równowagi bryły sztywnej możemy punkt zaczepienia siły przenieść dowolnie wzdłuż prostej działania tej siły.

Wypadkowa dwóch sił nierównoległych na płaszczyźnie

/| Na rys. 1.4 przedstawione są dwie siły, których proste działania przecinają się. Siły te można przesunąć do punktu A przecięcia się prostych działania tych sił i złożyć je, budując równoległobok sił

ABDC. Przekątna równoległoboku, jest siłą wypadkową W, sił Ą i P₂.

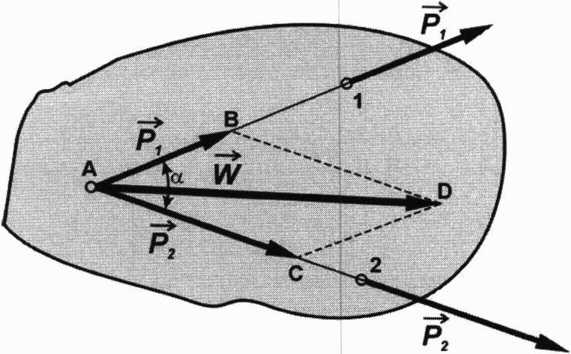
Rys. 1.4 Wypadkowa dwóch sił nierównoległych

Wartość liczbową siły wypadkowej można obliczyć z trójkąta sił pokazanego na rys.5. Ponieważ cos(l 80° — a) = — cos a , na podstawie twierdzenia cosinusów (twierdzenie Carnota) otrzymujemy:

			2	.	2
w	=v	p,	+	p2	+ 2	p,	p

cos a

(I-D

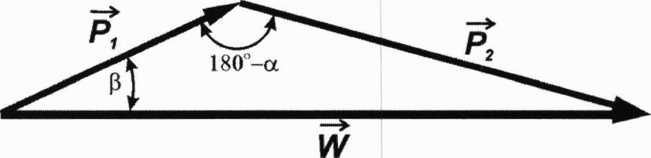
Rys. 1.5 Trójkąt sił do wyznaczenia siły wypadkowej

Prostą działania wypadkowej możemy określić za pomocą jednego z kątów, jakie tworzy ona z prostymi działania sił składowych (rys. 1.5). Z twierdzenia sinusów mamy:

sin fi =

sin«

W

(1.2)

^Aksjomat A)Moduł i prostą działania siły wypadkowej dwóch sił nierównoległych działających na ciało sztywne określa przekątna równoległoboku zbudowanego na wektorach sił składowych.

W szczególnych przypadkach mamy:

- 10-