CCF20130109016

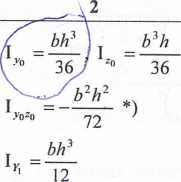
cd. tablicy I

^y₀

X X

3
©	>v0
	^©

i _t _nr _nd vo ~

U=o

64

*^ł> Znak momentu dewiacji dlii ćwiartki koła ustalamy analogie/ nie jak dla trójkąta.

I = I

-^V1 ^z0

!.v„ =

97T"

nr

~

nd⁴

TTŚT

-64 ₄ -r =

12n 9n² —64

" 16

12n

=0

.    .    97T-64 ₄

^I-^=I-^=_Msr^{r =}

_ 9;r² -64 1447T    ' 16

32-9;r

12n

	32-9n	^ *
	12n	16
V	= 1 ^Z| 16	nd^4~ 256
	r^4	</^4
	8	128

I =1    -*(*'-^r‘)

V₀ *0    ₄

_n(P⁴-d⁴)

=°

* i' 'U.I.AD I

¹ llur.lić główne centralne momenty bezwładności pola prostokąta pokazanego iiii i \ .miku 2.4a.

Ml

b)

c)

l\^zo

7

x-^L

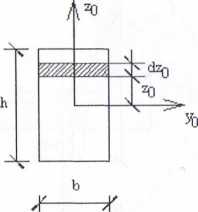
Rys. 2.4

*0

30^	\ f	f	/Sb
	✓
		1
		1

i^{1 2} li limy pole figury na paski o szerokości b i wysokości dzo (rys. 2.4b) oraz na , i l iii ./erokości dy₀ i wysokości h (rys. 2.4c). Pola elementarnych pasków wy-i odpowiednio:

. / I,    , dA₂ = hdy₀

il i,i u n-nic powyższego do zależności (2.5) daje:

li

h

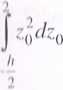
2

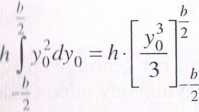
24    24

b³/z 12 ‘

h

b •	O OJ _1	? =b	1 *1 + r*A |
	1 u> 1_	h	24 24

blr

12 ’

i szerokości

(rys. 2.5c). b

1

KI Al) 2

2

i )M u /yć osiowe momenty bezwładności oraz moment dewiacji trójkąta prosto-i ,m, |ui pokazanego na rysunku 2.5, względem osi pokrywających się z bokami .. 11)| ,(in oraz osi centralnych.

11 / m I nny pole trójkąta na paski o wysokości dz

3

,|• i m.i/ paski o wysokości dy i szerokości