CCF20130109076

Współczynnik a zależy od kształtu przekroju i wynosi:

dla kątowników	a = 1,00
dla dwuteowników	a = 1,20
dla teowników	a = 1,15
dla ceowników	a = 1,12

Największe naprężenie styczne występuje w środku długości tego elementu przekroju, który ma największą grubość i wynosi

max

^zs

M-8„

h

(6.54)

Aby obliczyć naprężenie w dowolnym elemencie przekroju należy do wzoru (6.54) podstawić w miejsce <5_max grubość 6 rozpatrywanego elementu. Rozkład naprężeń stycznych w pręcie o przekroju wąskiego prostokąta pokazano na rysunku 6.69a.

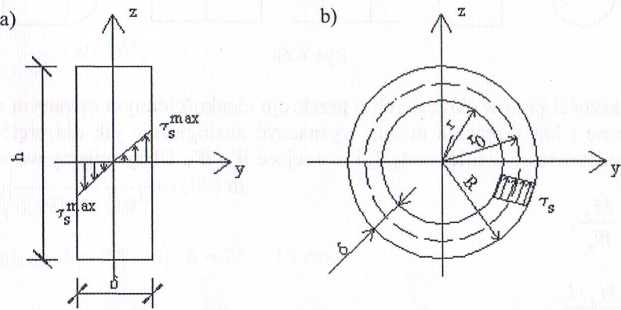
Rys. 6.69

Do obliczania prętów cienkościennych o przekroju zamkniętym można wykorzystać zależności stosowane dla przekrojów rurowych o małej grubości. Przyjmując, że promień zewnętrzny rury wynosi R, wewnętrzny r, grubość 8, a pro-

.,,    R+r

micn średni r_n =-

⁰ 2

oraz uwzględniając, że R-r = 8, otrzymujemy

Io=f(*⁴-'-⁴)=f(*²+r²)-2-V<5.

Podstawienie R = H—S

2

r_n -

1

2

8

daje

W₀ = 2n- r^S = 2A₀8,    ((

gdzie:

Aq - pole ograniczone promieniem średnim (linią konturu),

8 - grubość ścianki.

Naprężenie styczne w przekroju rozpatrywanego pręta wynosi zatem M_x M_r

Tc =—^Ł =-—.    (f

W₀    2 A₀8

Maksymalne naprężenie występuje w miejscu najmniejszej grubości ścianki ^max _ M_x

^Ts ~ _s    -    (t

Kąt skręcenia obliczamy ze wzoru

M-l M-l

(p = --- = -^- .    (6

GI₀ G-2Ąr₀<S

Mnożąc licznik i mianownik przez 2z ■ r₀ = S i podstawiając A₀-n- r₍₎² ot mujemy

(6

M_x S-l 4G ■ A] ■ 5 ’

gdzie:

5- obwód przekroju mierzony po linii konturu.

Powyższy wzór jest słuszny dla elementów o stałej grubości ścianki (5 = const

Otrzymane zależności można stosować przy obliczaniu prętów cienkościcnr zamkniętych, o dowolnym przekroju. Rozkład naprężeń w pręcie o przekroju c kościennym zamkniętym pokazano na rysunku 6.69b.