DSC00056 (19)

cłach

i ^A wyznacza całka

c_vx

-5

d A

746/

JTT

- 1

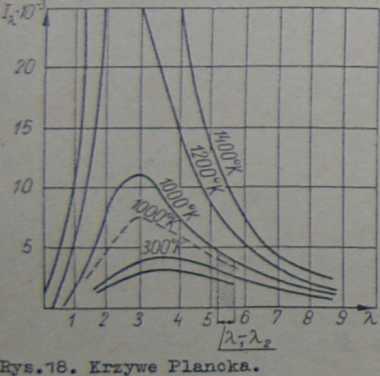
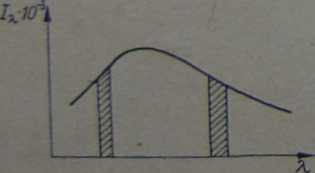
Ha 176*18 dla T = *1000°K jest "to pole zakreskowane•

Energię promienistą cia

ła czarnego dla całego widma wyznacza całka

V

-5

— dA /ą7/

- 1

Energia emitowana jest mniejsza dla ciał szarych niż dla ciał czarnych /na rys. 18 linia przerywana przedstawia krzywą Plancka dla T « 1000°K/.

Dla gazów energia emitowana może być ograniczona tylko do pewnych

długości fali /rys#19/• Informacje o tym w jakim zakresie promieniuje gaz — daje analiza spektralna.

Jeśli zróżniczkować równanie Plancka i przyrównać je do zera, to znajdujemy charakterystyczne maksima intensywności promieniowania • Wartość maksimów wyraża wzór

A ||§|g| « 0,002885 m.°K /48/

W ten sposób otrzymujemy prawo Wiena, które stwierdza,że ze wzrostem temperatury maksi— mum energii promienistej przesuwa się w kierunku fal krót-

Bys»‘19» Krzywa Plancka dla    szych. Dla źródeł ciepła o

gazu.

temperaturach praktycznie stosowanych w technice chemicznej, maksima te znajdują się w podczerwieni w niewidzialnej części widma.

2.3.4. Prawo Stefana—Boltzmanna

Przez scałkowanie równania /43/ można określić energię wypromieniowaną przez jednostkę powierzchni ciała doskonale czarnego we wszystkich długościach fali w temperaturze T

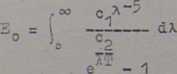
Na drodze odpowiednich przekształceń matematycznych całkę tę można doprowadzić do następującej postaci

= @.T⁴    /50/

gdzie 6 = 4,9,10“⁶kcal/n².h.°E^/5,68.10”⁸ -J~«/ - jest sta-łą promieniowania ciała doskonale czarnego. * ^&

Tak więc, w myśl wzoru /50/, prawo Stefana-Boltzmanna stwierdza, że energia emitowana przez ciało doskonale czarne jest proporcjonalna do czwartej potęgi temperatury bezwzględnej.'

Oczywiście dla ciała szarego

E=£.6.T⁴'    /91/

2.3.5. Prawo Lamberta

Według Lamberta energia wypromieniowana przez płaską powierzchnię w kierunku skośnym zmniejsza się proporcjonalnie do cosinusa kąta odchylenia /albo można powiedzieć, że ener -gia ta ma taką wartość, jakby promieniował rzut tej powierzchni na płaszczyznę prostopadłą do kierunku skośnego/. Prawo Lamberta ilustruje rys. 20a.

Niech będą dwie elementarne powierzchnie dF^ i dP₂

29