DSC00715

W przypadku ruchu ciała po powierzchni siłę tarcia kinetycznego można zapisać wgoretn

r*-|ł*Ar,

gdzie - współczynnik tarcia kinetycznego.

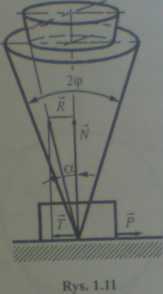
Na rysunku 1.11 przedstawiono uproszczony obraz przestrzenny, na którym linia działania siły czynnej P może przyjmować dowolny kierunek w ramach pełnego kąta 2n. W ten sposób linie działania wektora reakcji całkowitej R utworzą pobocznicę okrągłego stożka, który nazywamy stożkiem tarcia. Ciało pozostanie w równowadze statycznej, gdy linia działania reakcji całkowitej będzie zawierała się w stożku tarcia.

1.4.2. Tarcie cięgien

Odmianą tarcia ślizgowego po powierzchni krzywoliniowej jest tarcie występujące między cięgnem opasującym nieruchomy walec lub cięgnem opasującym ruchomy krążek, którego wał obciążony jest momentem obrotowym M₀ (rys. L12a i 1.12b).

Cięgno opasuje walec (krążek) o promieniu r na długośd łuku ABC, któremu odpowiada kąt opasania a. Końce cięgna obciążone są siłami S, i Ś₂, z których siła S, w przypadku walca jest siłą czynną, tzn. taką, która mogłaby spowodować poślizg cięgna po powierzchni walca, a siła S₂ jest siłą bierną, równoważącą. W przypadku krążka obydwie siły są siłami reakcji, przy czym S₍ jest siłą większą. Pomiędzy powierzchniami cięgna i walca (krążka) występuje tarcie ślizgowe, którego wartość zależy od wartości współczynnika tarcia p i wielkości kąta opasania a. Rozwiązanie zadania polega na wyznaczeniu funkcji Sj =/(Sj, p, a). Zadanie rozwiążemy, rozpatrując równowagę elementarnego łuku cięgna dS, któremu odpowiada elementarny kąt