DSC03087

& . II-I.    i..

—

Xj Pressure Dismbution in a Fluid 1|

consider that a hcight difference of 1 cm in a fluid with SG = 0.85 corresponds to a pressure difference of S3.2 Pa. In Fig. P2.42. what difference p_A — p_B conesponds to h = 1 * cm w hen SG, = 0.84 and SG₂ = 0.86? What is the increase in accuracy?

Water flows downward in a pipę at 45°. as shown in Fig. P2.44. The pressure drop p, — p₂ is partly due to gravity and partly due to friction. The mercury manometer reads " a 6-in height difference. What is the total pressure drop p, - Pj in Ibf/in³? What is the pressure drop due to friction — only between 1 and 2 in Ibf/in³? Does the manometer read-ing correspond only to friction drop? Why?

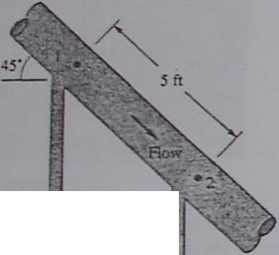
Water

Mercury

Ftg.P2.44

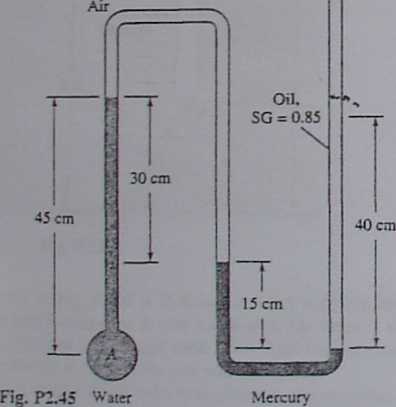
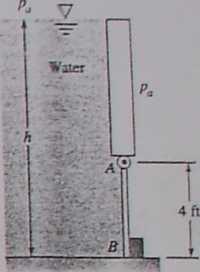
Detennine the gage pressure at point A in Pa. Is it higher or lower than atmospheric?

Pian

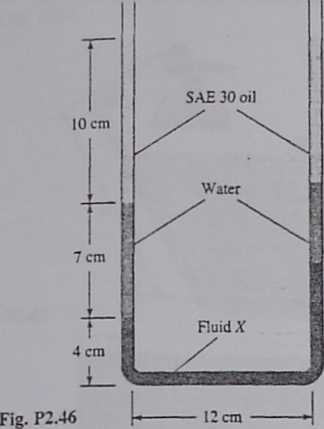
1.46 In Fig. P2.46 both ends of the manometer are open to the

atmosphenr. Estimate the specific gravity of fluid X.

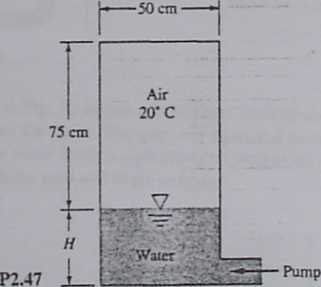
2.47 The cylindrical tank in Fig. P2.47 is being filled with water at 20°C by a pump developing an exit pressure of 175 kPa. At the instant shown. the air pressure is 110 kPa and H = 35 cm. The pump stops when it can no longer raise the water pressure. For isothermal air compression, estimate H at that dme.

2.48    Repeat Example 2.5, but instead let the hinge be at point A and let point B rest against a smooth bottom.

2.49    A vertical gate 6 ft wide and 8 ft high is hinged at the top and held closed by water, on one side, whose level is 7 ft above the gate top. What horizontal force applied at the bottom of the gate is required to open it? Neglect the atmospheric.pressure effecL

2 jO A vat filled with oil (SG = 0.87) is 6 m long and 4 m deep and has a trapezoidal cross section 3 m wide at the bottom and 5 m wide at the top. Compute (a) the weight of oil in

Problems 95

ihc vat, (b) the force on the vat bottom. and (c) the force on the trapezoidal end panel.

2J51 Gate AB in Fig. P2.51 is 1.2 m long and 0.8 m into the paper. Neglecting atmospheric pressure, compute the force F on the gate and its center-of-pressure position X.

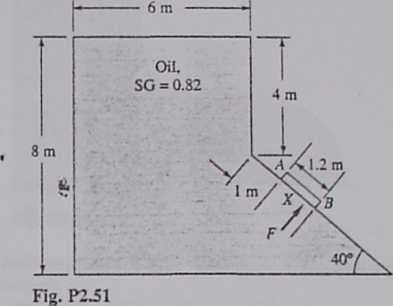
2.52    Suppose that the tank in Fig. P2.51 is filled with liquid X, not oil. Gate AB is 0.8 m wide into the paper. Suppose that !iquid X causcs a force F on gate AB and that the moment of this force about point B is 26.500 N • m. What is the specific gravity of liquid XI

2.53    Figurę P2.53 shows the elevation and right-side views of an open tank. If the tank is filled with water at 20°C, compute (a) the force of the water on panel ABC and (b) the moment of this force about linę AB.

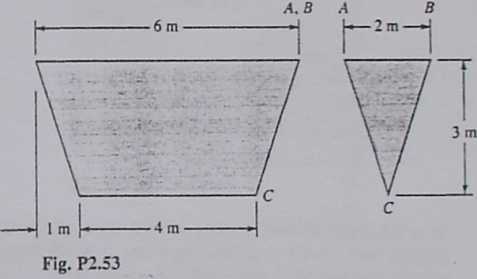
2.54    Figurę P2 J3 shows the elevation and right-side views of an open tank. If the tank is filled with liquid X, the force of the liquid on panel ABC is found to be 26 kN. Compute (a) the moment of this force about linę AB and (6) the specific grav-ity of liquid X.

2.55    Gate AB in Fig. P2.55 is 5 ft wide into the paper, hinged at A. and restrained by a stop at B. The water is at 20°C. Compute (a) the force on stop B and (b) the reactions at A if the water depth h — 9.5 ft.

Fig. P2.55

U6 In Fig. P2 .55, gate AB is 5 ft wide into the paper. and stop B will break if the water force on it equals 9200 lbf. For what water depth h is this condition reached?

1S1 In Fig. P2.55, gate AB is 5 ft wide into the paper. Suppose that the fluid is liquid X, not water. Hinge A breaks when its reacdon is 7800 lbC, and the liquid depth is h — 13 ft. What is the specific gzavity of liquid XP.

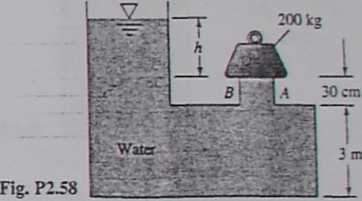
2.58 In Fig. P2.58 the cover gate AB closes a circular opening 80 cm in diameter. The gate is held closed by a 200-kg mass as shown. Assume standard gravity at 20°C. At what water level h will the gate bedislodged? Neglect the weight of the gate.

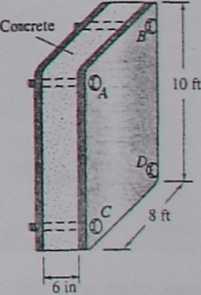
2^9 When freshly poured between wooden forms, concrete ap-proximates a fluid vżńi SG = 2.40. Figurę P2Ó9 shows an

Fig. P2.59

A 23