DSCN0765

Rys. 2-61. Rysowanie epicykloidy

2.6.4. Hipocykloida

Hipocykloidą nazywamy krzywą, która powstaje przy toczeniu się koła po wewnętrznej strome okręgu drugiego koła. Konstrukcję wyjaśnia rys. 2-62.

Ryś. 2-62. Rysowanie hipocylgjidy

2.7. KRZYWE SPIRALNE. SPIRALA ARCHIMEDESA

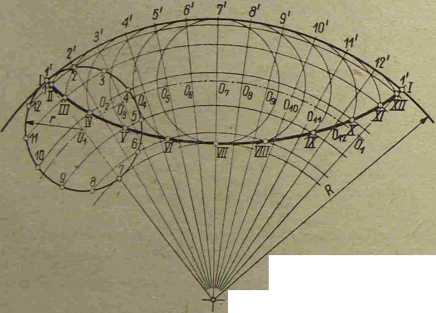
Jeżeli dowolny punkt A porusza się ruchem postępowym ze stałą prędkością po promieniu, który jednocześnie obraca się ze stalą prędkością kątową około środka O, to wypadkowy ruch punktu A odbywa się po linii krzywej, zwanej spiralą Archimedesa. Spirale mogą być jedno- r \yielokrotne w zależności od

podziału promienia na żądaną liczbę równych części, a poza tym spirale mogą być prawo- lub lewoskrętne.

Rys. 2-63. Rysowanie spirali Arcbimedesa

Dany okrąg dzielimy np. na osiem równych części i punkty podziału łączy--my. ze środkiem O (rys. 2-63). Na tę samą liczbę części dzielimy promień. Przez punkty podziału promienia prowadzimy ze środka O luki w następujący sposób: promieniem Ol zakreślamy łuk do przecięcia się z promieniem Ol, promieniem Oli do przecięcia się z promieniem 02 itd.

Otrzymane w ten sposób punkty wyznaczają szukaną krzywą. Spirala Archimedesa ma szerokie zastosowanie w technice. Kszta¹1 spiralny mają różnego rodzaju krzywki, sprężyny, rowki w płytkach szamotowych kuchenek elektrycznych, zaciski mi-mośrodowe itp. Spirali logarytmicznej i hiperbo-licznej nie będziemy omawiać.

2.8. LINIA ŚRUBOWA

. Jeśli na powierzchnię walca o średnicy d nawiniemy trójkąt prostokątny, którego jedńa przyprostokątna AB = 7id, a druga CB = h, to przeciwprosto-kątna AC wyznaczy linię śrubową cylindryczną. Rys. 2-64 podaje sposób wykreślenia linii śrubowej prawoskyętnej i lewoskrętnej.

Rys. 2-64. Rysowanie linii śrubowej