DSCN0794 (2)

C"D", który jest pionowym rzutem małej osi elipsy CD. Do odnalezienia ^ poziomego tej osi podążymy się pomocniczą płaszczyzną równoległą do ni ji_p której ślad pionowy ty przejdzie przez punkty C"D". Płaszczyzna /

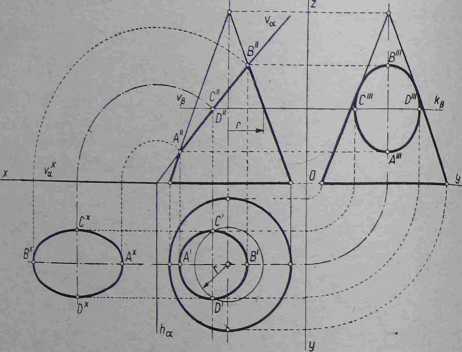
Rys. 4-60. Stożek przecięty ukośnie, kład figury przecięcia na rzutnię poziomą

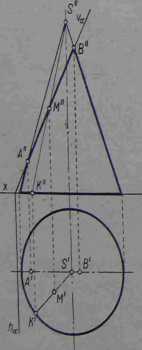
Rys. 4-61. Wyznaczanie rzutów przecięcia stożka za pomocą tworzących pomocniczych

przetnie powierzchnię boczną stożka według okręgu o promieniu r rzutującego I się na poziomą płaszczyznę w wielkości rzeczywistej, a płaszczyznę a wg pros- j tej prostopadłej do rzutni pionowej. Poziomy rzut J tej prostej jest więc prostą prostopadłą do osi X. I Przecięcie się okręgu z prostą wyznaczy rzut I poziomy CD' małej osi elipsy. Mając rzut piono- I wy i poziomy małej osi elipsy, łatwo znajdziemy jej j rzut boczny C" D'". W ten sposób znaleźliśmy I rzuty poziome i boczne obu osi elipsy.

Konstrukcję krzywej wykonać możemy jed- | nyin ze znanych sposobów (patrz p. 2.5.1.) i w ten sposób otrzymać poziomy i boczny rzuty przecięcia stożka. Aby znaleźć rzeczywistą wielkość figury przecięcia, doprowadzamy płaszczyznę - a do kładu z rzutnią poziomą i znanym sposobem odnajdujemy rzeczywistą wielkość figury przecięcia.

Na rys. 4-61 przedstawiono inny sposób wy* znaczania rzutów przecięcia polegający na posługiwaniu się pomocniczymi tworzącymi stożka. Na poziomym rzucie stożka obieramy poziomy rzut dowolnej tworzącej S'K', a następnie znajdujemyj^ej rzut pionowy. S"K'\ który przetnie się ze śladem

pionowym płaszczyzny w punkcie M". Mając rzut pionowy M" przecięcia się płaszczyzny tnącej z tworzącą stożka, opuszczamy z tego punktu prostopadłą do osi * i na przecięciu z rzutem poziomym tej tworzącej znajdujemy poziomy rzut M' punktu należącego do przecięcia stożka.

Na rys. 4-62 obraliśmy osiem punktów należących do figury przecięcia. Rozwinięcie powierzchni bocznej uciętego stożka wykonujemy kreśląc wycinek kola o promieniu równym tworzącej l pełnego stożka i o kącie przy wie

gdzie D — średnica podstawy, l —

rzchołku obliczonym ze wzoru a = 180° —

tworząca stożka (długość luku równa się obwodowi podstawy stożka). Łuk wycinka dzielimy na taką samą liczbę równych części, co i podstawę stożka (w naszym przypadku na 8), łącząc punkty podziału z wierzchołkiem wycinka S. Znanym sposobem określamy rzeczywiste długości każdej tworzącej uciętego stożka i odkładamy j e na prostych łączących punkty podziału luku wycinka z wierzchołkiem S. Otrzymane w ten sposób punkty I „ 2_lt 3₁ itd. łączymy za pomocą krzywika.

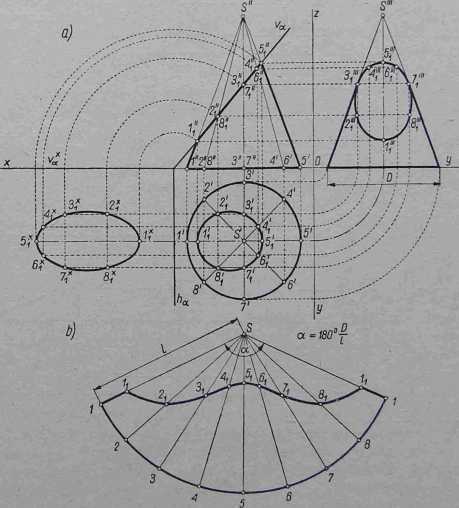
Rys. 4-62. Stożek przecięty płaszczyzną pionowo rzutującą: o — rzuty, kład przekroju, b — rozwinięcie powierzchni bocznej

85