DSCN1152 (2)

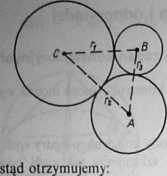
Rys. 6.1

^rt = \(^di + d₂-d₃),r₂ = -{d_l ~^dl ^{+ i}l>' r, = ii{-d_l +d₂ + d₃).

Zadanie ma zawsze dokładnie jedno rozwiązanie.

6.2.    Niech A będzie środkiem okręgu stycznego wewnętrznie do okręgów o środkach B i C. Niech r,, r₂, r₃ oznaczają długości promieni okręgów odpowiednio o środkach A, B, C.

Wówczas

^ri = \(^di + d₂ + d₃\r₂ = -(~d_t + d₂ + d₃^r₃-^(d₂ -d₂ + d₃\

gdzie d, = {AB\; d₂ = \AC\ i d₃ = \BC\.

Zadanie ma zawsze trzy rozwiązania.

6.3.    Zadanie ma rozwiązanie jedynie w przypadku, gdy punkty A i B leżą po tej samej stronie prostej k.

Zauważmy, że środek szukanego okręgu leży na symetralnej odcinka AB. Mamy wtedy dwa przypadki:

1)    symetralna odcinka AB jest równoległa do prostej k,

2)    symetralna odcinka AB przecina prostą k.

W przypadku 1) rozwiązaniem będzie każdy z dwóch okręgów, których:

-    promień jest równy odległości r między prostą k i symetralną odcinka AB,

-    środek jest odległy o r od punktów A i B.

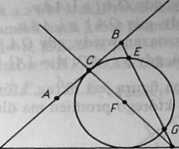
W przypadku 2) niech C będzie środkiem AB, D - punktem przecięcia prostej k i symetralnej odcinka AB, F - środkiem okręgu stycznego do prostych k i AB leżącym na prostej CD (rys. 6.3). Niech

D

Rys. 6.3

E i G będą punktami wspólnymi odcinka BD i okręgu o(F. |FC|) (w przypadku, gdy AB\\k punkty D i G pokrywają się). Szukanym okręgiem będzie

ijcrl (o(F, |FC|) lub ij^t (o(F, |FCI)).

W przypadku, gdy,4B||k mamy do czynienia tylko z tym pierwszym okręgiem.

Środkiem okręgu jest zatem punkt Pe CD taki, że PBUEF lub punkt QeCD taki, że QB\\GF.

Zadanie ma dwa rozwiązania, gdy ABftk, oraz jedno rozwiązanie, gdy AB\\k.

6.4. Przypuśćmy, że skonstruowaliśmy poszukiwany okrąg i że jest nim okrąg o(S.R) (rys. 6.4).

^ Rys. 6.4

Niech L będzie punktem styczności okręgu iĄS, R) z prostą p, zaś K - punktem wspólnym prostej p i stycznej do danego okręgu

w punkcie A. Ponieważ |/tS| = |SZ. | = R. | < K,4S| = |< SL K| = ^,

więc trójkąty SAK i SKL są przystające. Zatem |KL | = \AK\. Stąd wynika konstrukcja. Zadanie ma:

1* — Zbiór ndiń . 161