Strona0142
142
gdzie:
|
Ą =^AU+Ai2 = ~^Di +D2 , |
-A <m=— |
|
^=1/ą2]+4=|-VjD2+o42. |
f Q" u £ W) |
Przejmujemy, źe dla układu pokazanego na rys. 6.5 k2~a2-cc1- 0, wówczas amplitudy mas mi i m2 wyrażają się następującymi wzorami:
Ą=Ą
(k-m2a>2)2 +a2co2
+ k-m^2-m2a)2}-k2J +a2(o2[[ml + m2)co2 -Aj1 J
' ĄsaPi_k2+aY _
+k-n\m2}(k~m2a)2^-k2J + «2ftr[(mI +m2)a)z -A2]2
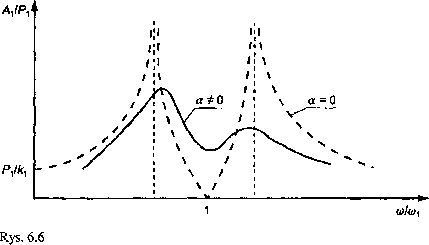
Ze wzorów (6.52) wynika, że amplitudy drgań wymuszonych obu mas pozostają ograniczone dla wszystkich wartości siły wymuszającej, jeśli w układzie występuje tłumienie a ^ 0. Przykładowe wykresy charakterystyk amplitudowo--częstotliwościowych pokazano na rys. 6.6.
Przykład 6.1
Wyznaczyć częstość własną małych drgań i postacie drgań normalnych układu o dwóch stopniach swobody (rys. 6.7a), pomijając siły oporu, masy sprę-
Wyszukiwarka
Podobne podstrony:
Strona0134 134 gdzie Au i Al2 - dowolne liczby (można np. przyjąć An = An -1), z którymi A2l i A22 s
Strona0149 149 gdzie: fi*=33,54s“ <a2 =40,87 s“ /i, =-0,314, ju2-12,01Zadanie 6.3 Dla układu mech
III.III. II., AO,o2 Ul,7_____ AQOG Uj,7 U, ,.7 IJ5.7 AU AOtOS di,7 W i, 5, i d2,7
Strona0128 128 Wprowadźmy następujące oznaczenia: Cx ~AU sin C2- Al2 sin ę2
Strona0032 32 ¥ (2.28) ±(E + V) = 0 di gdzie: E - energia kinetyczna układu, V- energia potencjalna
Strona0140 140 gdzie: mx,m2 - masy drgające, klyk2,k - współczynniki sprężystości, ax, a2, a - współ
gdzie D, jest dywidendą za rok t. Przypadki wzrostu dywidendy. a) wzrost zerowy - w tym przypadku Di
skanuj0019 (113) ćwiczenie C4 (strona 152) ćwiczenie A10 (strona 142) ćwiczenie Ali (strona 143) l!B
Strona00142 - 142 - 127. Przeć enlacz mikrofonowy z wzmacnia ozem operacyjnym Schemat powyższy przed
gdzie: AU - spadek napięcia na twomiku Wprowadzając do wzoru (10) zależność (7),
142 gdzie: i - ilość stopni swobody, n - ilość składników, /- ilość faz, p - ciśnienie. Przy
Scan449 5C, skąd obliczamy D2 = VA = 50,0kN Korzystając dodatkowo z warunku równowagi węzła 2 IX2 =
więcej podobnych podstron