DSCN1159 (2)

6.28. Wskazówka. Załóżmy, że znaleźliśmy szukany punkt M. Wówczas na podstawie twierdzenia sinusów mamy:

I ■ li fg _JB£l_ _{= 2r}

sinH:/lMC| | sinKBMCl ²’ gdzie r, jest promieniem okręgu opisanego na trójkącie AMC, zaś r₂ - promieniem okręgu opisanego na trójkącie BCM. Ponieważ sin | -fc AMC\ = sin| BMC\ = sina, gdzie a = | < BMC| więc

\AC\ + \BC\ ,    . \AC\ + \BC\

r, + r, =^;——-, skąd sina =--.

2sma    2d

Zadanie ma rozwiązanie wtedy, gdy \AC\ + \BC\ < 2d.

Przy czym

1)    jedno rozwiązanie wtedy, gdy |>4C| + |BC| = 2d,

2)    dwa rozwiązania, jeśli \AC\ + |BC| < 2d.

6.29. Niech jednym z prostokątów rodziny będzie prostokąt KLMN (rys. 6.291.

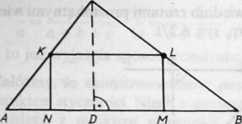
Rys. 6.29

Oznaczmy |/CN| = x i załóżmy, że \AB\ = a, zaś |CD| = h.

Ponieważ A.ABC ~ AKLC.

więc

Jeśli przez d oznaczymy długość przekątnej prostokąta KLMN,

_rfw-A-*>^ł,

h^Ł

więc

d² =

(h² + a²)x² — 2arhx + a²h²

d(x) = tn/(/i² i a²)x² - 2a¹hx + a²h¹.    11

n

Jak nietrudno obliczyć, funkcja d osiąga najmniejszą wartość dla a²h

^{X =} a + h²'

Wtedy to: |KL| = ■

ah    d²

i d =    , = ■■■-.. oraz x = —.

Ja² + h²    h

ah²

■ a² + /i²

Również nietrudno zauważyć, że ^/a² + h² jest przeciprostokąt-ną trójkąta prostokątnego o przyprostokątnych a. h. Wtedy d jest wysokością tego trójkąta poprowadzoną z wierzchołka kąta . x d prostego ^l2~h'

Wynika stąd konstrukcja:

1)    Konstruujemy kolejno odcinki o długościach d oraz x,

2)    Kreślimy prostą której odległość od prostej AB jest równa x. Prosta ta przecina boki AC i BC odpowiednio w punktach K, L.

3)    Znajdujemy rzuty prostokątne N, M punktów K, L na prostą AB. Prostokąt KLMN jest szukanym prostokątem.

Zadanie ma rozwiązanie, gdy | -£.41 ^ ^ i | <B| $

6.30. Niech CD będzie wysokością A ABC, F - środkiem tej wysokości a E - środkiem boku AB.

Niech WZTU będzie takim prostokątem, że UeAC; Te BC; W,Ze AB.

Niech R i S będą środkami boków UTi WZ prostokąta. Odcinek RS przecina EF w punkcie X. Ponieważ EF jest środkową boku DC trójkąta DEC. więc X jest środkiem RS, czyli środkiem prostokąta WZTU. Wykazaliśmy, że środek dowolnego prostokąta rodziny P leży na odcinku EF.

Przypuśćmy obecnie, że mamy pewien punkt XeEF. Poprowadźmy przez punkt X prostą RS|| CD (gdzie Re CE i Se AB) oraz prostą X Y\\AB(YeBF). Przez punkt /poprowadźmy prostą

175