DSCF6533

2. OPRACOWANIE WYNIKÓW POMIARÓW

2.1. Zmienna losowa

Zdarzeniem losowym nazywamy zdarzenie, które ma więcej niż jedną możliwą realizację. Wynik takiego zdarzenia jest nieprzewidywalny, znane mogą być jedynie prawdopodobieństwa zajścia możliwych wariantów. Na przykład wynik rzutu symetryczną monetą może się okazać orłem lub reszką, z prawdopodobieństwem P₀ = P_r = 0,5 dla monety wystarczająco cienkiej, aby można zaniedbać możliwość „wypadnięcia” krawędzi. Podobnie rzut prawidłową kostką do gry może dać z prawdopodobieństwem 1/6 każdy z sześciu możliwych rezultatów. Wynik każdego eksperymentu (pomiaru) jest zdarzeniem losowym. Ze zdarzeniem losowym wygodnie jest skojarzyć zmienną losową X, mogącą uzyskiwać wartości liczbowe x_t, x₂, odpowiadające możliwym rezultatom pomiaru. Odpowiednie prawdopodobieństwa P(x_i), P(x₂),... tworzą rozkład prawdopodobieństwa. Zależnie od tego, czy wynikiem mogą być dowolne, czy tylko niektóre wartości z dozwolonego przedziału, mówimy o zmiennej losowej ciągłej lub skokowej (dyskretnej).

Funkq'ę/(x), charakteryzującą prawdopodobieństwo przyjęcia przez zmienną losową wartości bliskiej x, nazywamy funkcją gęstości prawdopodobieństwa albo po prostu rozkładem. Ponieważ prawdopodobieństwo znalezienia zmiennej w wąskim przedziale dx: Prób {Xe(x,x+ dx)} = P(x, x + dx) dąży do zera wraz z szerokością przedziału, prawdopodobieństwo tego, że zmienna losowa ciągła ma wartość dokładnie równą x, wynosi 0. Funkcję J[x) określa się zwykle pośrednio, interpretując „iloczyn” J[x)dx, jako prawdopodobieństwa przyjęcia przez zmienną losową X wartości z przedziału (x,x + dx):

Prób {X e(x,x + dx)} = P(x, x + dx)= J{x)dx    (2.1)

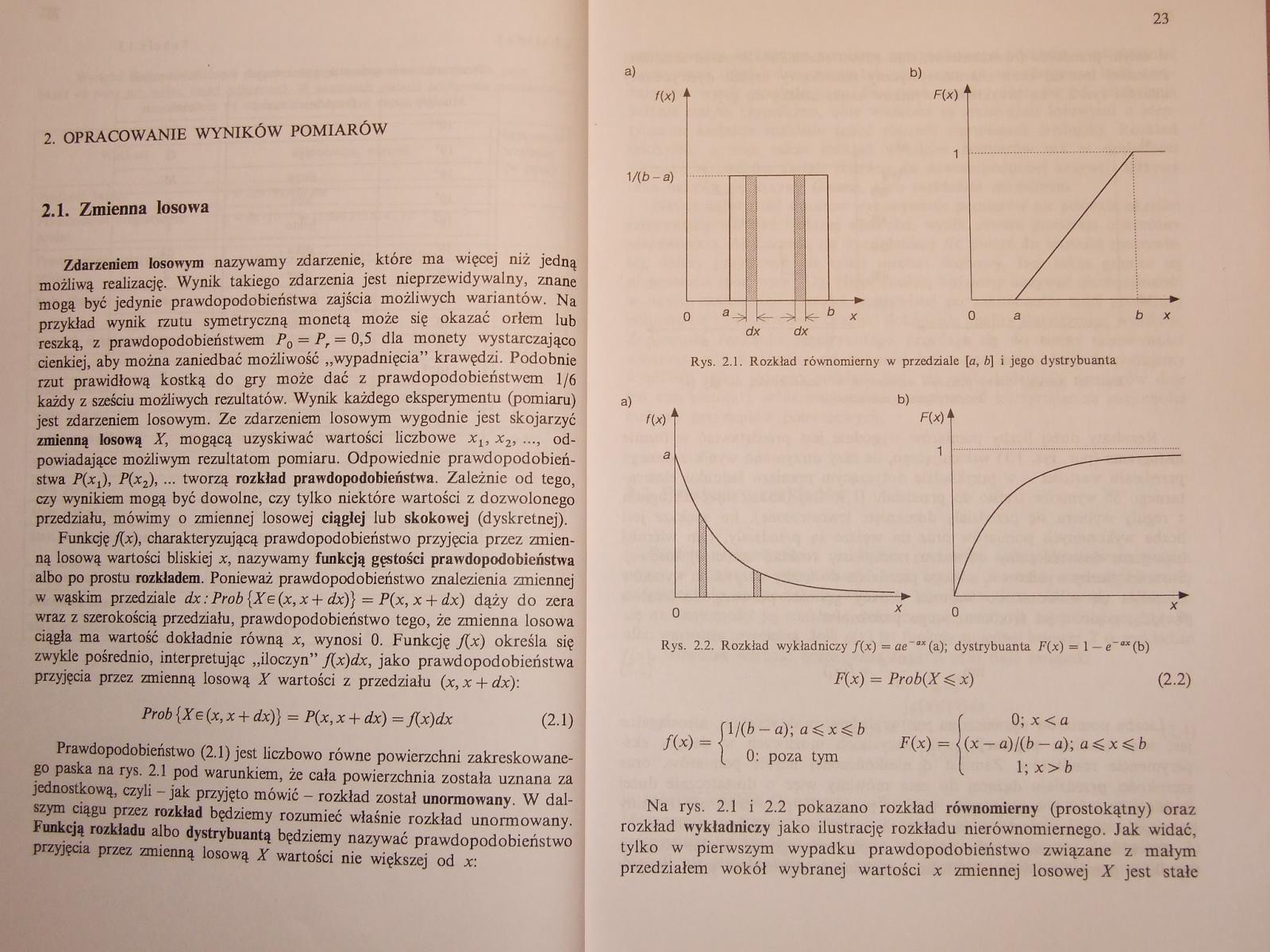
Prawdopodobieństwo (2.1) jest liczbowo równe powierzchni zakreskowane-go paska na rys. 2.1 pod warunkiem, że cała powierzchnia została uznana za jednostkową, czyli - jak przyjęto mówić - rozkład został unormowany. W dalszym ciągu przez rozkład będziemy rozumieć właśnie rozkład unormowany. Funkcją rozkładu albo dystrybuantą będziemy nazywać prawdopodobieństwo przyjęcia przez zmienną losową X wartości nie większej od x:

a)    b)

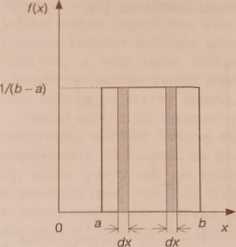
Rys. 2.1. Rozkład równomierny w przedziale [a, b] i jego dystrybuanta

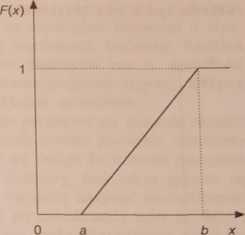
Rys. 2.2. Rozkład wykładniczy f{x) =ae “(a); dystrybuanta F(x) = 1 — e”“(b)

(2.2)

Ąx) = Prob(X < x)

l/(b — a); a<x<ó 0: poza tym

/(*) =

r 0; x < a

F(x) = | (x — a)/(ł> — a); a < x < b | l;x>b

Na rys. 2.1 i 2.2 pokazano rozkład równomierny (prostokątny) oraz rozkład wykładniczy jako ilustrację rozkładu nierównomiernego. Jak widać, tylko w pierwszym wypadku prawdopodobieństwo związane z małym przedziałem wokół wybranej wartości x zmiennej losowej X jest stałe