DSCF6589

134

Po dokonaniu niezbędnych pomiarów (średnica kapilary i naczynia) należy zbadać zależność wysokości wzniesienia słupa wody w kapilarze od temperatury, zmieniając temperaturę co ok. 5 K. Następnie w temperaturze pokojowej należy zmierzyć wysokość wzniesienia słupka innej cieczy (np. nafty).

6. Opracowanie

W oparciu o wyniki pomiarów należy wykreślić zależność napięcia powierzchniowego wody od temperatury a = a(T). Na podstawie wzorów 21 i 22 szacujemy wymiary cząsteczek wody i nafty oraz liczbę Avogadro, W obu tych wzorach nie występuje temperatura, co wyraźnie wskazuje na ich przybliżony charakter. Do obliczeń wykorzystujemy wartości napięcia powierzchniowego, znalezione w temperaturze pokojowej.

Pytania

1.    Wprawdzie we wzorach 21 i 22 nie występuje explicite temperatura, można jednak zauważyć możliwość przybliżonego kompensowania się zmian termicznych a i c_p takiego, aby obliczone wartości d i N_A pozostawały niemal stałe. Jaka to możliwość?

2.    Jakiej korelacji należy oczekiwać pomiędzy wartościami napięcia powierzchniowego i ciepła parowania cieczy?

C-5. Pomiar ciepła właściwego powietrza metodą rozładowania kondensatora [26]

1. Wstęp

Jeśli do układu dostarczamy ciepło dQ za pośrednictwem procesu, w którym temperatura wzrasta o dT, a zachowuje się pewna wielkość x, wówczas wyrażenie:

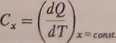
„arywamy pojemnością cieplną układu dla stałego x. Gdy x = p, mówimy ₀ pojemności cieplnej przy stałym ciśnieniu, gdy x = V - o pojemności jjplnej przy stałej objętości. Pojemność cieplna odniesiona do jednostki -asy, nazywa się ciepłem właściwym; pojemność cieplną jednego mola „jiywamy ciepłem molowym. Ciepło właściwe przy stałym ciśnieniu i przy _st3jej objętości określają wzory:

I m{dr) p^con,,    ^(2a)

Itslfik.    1

;dzie m oznacza masę układu.

W wypadku dostarczania ciepła przy stałym ciśnieniu, z 1 zasady ttnnodynamiki wynika związek:

dQ_p = dE + dW= dE + pdV    (3)

JE oznacza tutaj przyrost energii wewnętrznej, dW - pracę wykonaną przez układ. Dla jednego mola gazu doskonałego pV= RT (R= 8,314lltólwK^-1) i pdV=RdT. Po podstawieniu tego związku do równania 3 otrzymamy:

dQ_p = dE + RdT    (4a)

albo po podzieleniu obu stron przez dT:

_ dE i

^CP=W^+R    (4b)

Jeśli ciepło dostarczane jest przy stałej objętości, wówczas dV= 0 i iQ_y = dE.

Postępując podobnie jak poprzednio otrzymamy:

B

Z porównania 4b i 5 otrzymamy tzw. związek Mayera:

(6)

C_p-Cy=R