DSCF6606

168

gdzie:

j = AT² exp

O)

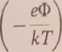
A = 4 nmek²n-³ = 1,23 • 10⁶ Am~²K~²

e® oznacza pracę wyjścia elektronu z metalu, /w i e oznaczają odpowiednio masę i ładunek elektronu, k - stałą Boltzmanna, a h stałą Plancka.

Wyprowadzenie równania termoemisji, zamieszczone w wielu podręcznikach (np. C. Kittel, Wstęp do fizyki ciała stałego, Warszawa 1976), jest niestety zbyt skomplikowane, aby je można było tutaj przytoczyć. Wspomnijmy tylko, że wzór 1 otrzymano stosując do opisu „gazu elektronowego" kwantową statystykę Fermiego-Diraca, zamiast klasycznej Maxwella-BoItz-manna. Model klasyczny ma jednak walor poglądowości i dlatego poświęcimy mu nieco uwagi.

Rozpatrzmy działanie lampy dwuelektrodowej - diody. Emitowane przez rozgrzaną katodę elektrony tworzą wokół niej ładunek przestrzenny (chmurę elektronową), pozostającą z katodą w stanie zbliżonym do równowagi - liczba elektronów wysyłanych przez katodę jest niemal równa liczbie elektronów powracających do katody z obszaru ładunku przestrzennego. Tylko elektrony opuszczające katodę z dużą prędkością docierają do anody. Jest to obraz bardzo przypominający parę nasyconą unoszącą się nad powierzchnią cieczy - model pierwotnie użyty przez Richardsona, w którym gaz elektronowy w metalu był traktowany jak ciecz, a elektrony tworzące ładunek przestrzenny jak gaz doskonały, stanowił rozwinięcie tej analogii. Wykorzystanie równania Clausiusa-Clapeyrona (por. ćw. C-9) pozwoliło na otrzymanie temperaturowej zależności gęstości prądu termoemisji w postaci

j = AT^1/2 exp

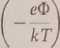
przy założeniu, że gęstość elektronów w metalu nie zależy od temperatury. Jeśli gęstość zmieniałaby się jak T^3/2, otrzymany związek byłby identyczny ze wzorem 1. Eksperymentalne znalezienie wartości wykładnika przy T wymaga dużej dokładności, ze względu na niską czułość wyników na wartość tego parametru - decydujący wpływ na zależność temperaturową ma czynnik wykładniczy

podatk°^we problemy stwarzają trudne do usunięcia zanieczyszczenia badanych ^ierzehni metalicznych, wpływ siatki krystalicznej zakłócający izotropię ^jIju elektronów, a także inne efekty, np. zjawisko wewnętrznego odbicia jlektronów.

^ yłetoda pomiaru

Ma wstępie rozpatrzyliśmy emisję elektronów tworzących ładunek prze-suzenny w pobliżu katody wówczas, gdy potencjał anody był bliski 0.

\V miarę wzrostu napięcia anodowego coraz więcej elektronów opuszcza obszar ładunku przestrzennego i dociera do anody. Przy dostatecznie dużym uapięciu anodowym prąd anodowy osiąga wartość nasycenia, zależną dla danej lampy tylko od temperatury katody. Katody współczesnych lamp elektronowych wykonywane są z materiałów o tak dużej wydajności (maksymalnej gęstości prądu termoemisji), że osiągnięcie prądu nasycenia w normalnych warunkach pracy powoduje zwykle uszkodzenie lampy. Dlatego doświadczenie będzie wykonywane przy niższych od nominalnej temperaturach katody. Wielkością bezpośrednio mierzoną będzie nie gęstość prądu termoemisji, lecz natężenie prądu nasycenia. Ponieważ obie wielkości są liniowo związane, oczekujemy, że temperaturową zależność prądu nasycenia opisuje wyrażenie:

foas. = BT ² exp(~^    (2)

gdzie 2? jest stałą „aparaturową”, zależną m. in. od pola powierzchni katody. Po zlogarytmowaniu obu stron wzoru 2 otrzymamy związek:

fc- ^l”(W ^{= lnB}-£ S

toóry dzięki zastosowaniu odpowiedniej skali funkcyjnej przyjmuje postać liniową:

y = a + bx    (4)

gdzie:

T²

y = ln

1

x = -

T