freakpp075

148

\3.1. Ustalone pola temperatury we współrzędnych prostokątnych

/...sadę budowania modelu analogowego pola temperatury typu - siatka elektiycma jest najłatwiej przedstawić dla płaskiego obszaru, podzielonego na jednak* ve prostokąty o bokach Ax i Ay (rys. 7.1). W wyniku dyskretyzacji równani różniczkowe Laplace’a

(7.3)

3²T a²T 3x² +3y²

przechodzi w równanie różnicowe, które dla węzła 0 siatki dy skręty żującej, otoczonego przez węzły 1,2, 3, 4, przybiera postać:

_{+    +    =} o    (7.4)

[Ax] [Ax] [Ay]' [Ay]

lub

^T1 - To + T₂ - Tq ₊ JWo ₊ T₄_-Tp _ ₀    (7.5)

Ax    Ax    Ay    Ay

Ay    Ay    Ax    Ax

Ax

	—f—	—?—		—*
	1	.....b
	.....|2.	io			JL..
								—	—
			►4-
	—i—		—		k—		L—

Rys. 7.1. Prostokątna siatka dyskretyżująca płaskie pole temperatury

$

komórka na płaskiej powierzchni zewnętrznej pola

komórka na krawędzi pola

komórka wewnątrz pola

brzeg obszaru

Równanie (7.5) jest analogiczne do równania różnicowego potencjałów elektrycznych siatki rezystorów (rys. 7.2), rozpiętych między węzłami 0, 1,2,

3, 4, które otrzymuje się z I prawa Kirchhoffa dla węzłów siatki elektrycznej, a mianowicie

^U1~^U0 , ^U2~^U0 ! ^U3~^0 _[ ^U4~^U0₌q Rl    R2    R3    R4

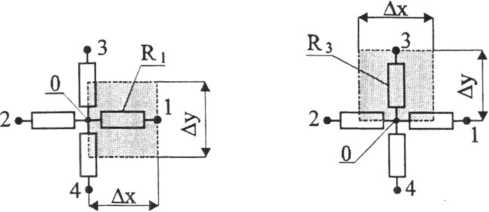
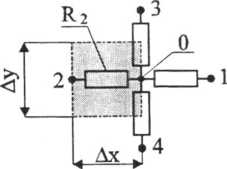
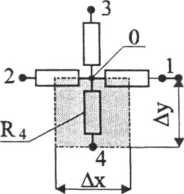
Rys. 7.2. Obszary modelowane przez poszczególne rezystory przy dyskretyzacji płaskiego pola siatką prostokątną

Analogia termiczno-elektryczna jest spełniona, gdy istnieje proporcjonalność temperatury do potencjału elektrycznego w odpowiednich węzłach siatki:

k_r = T/U    (7.7)

oraz proporcjonalność oporów cieplnych R_t, odpowiednich obszarów dyskretyzacji i rezystancji oporników siatki elektrycznej R:

(7.8)

k_R = R,/R

gdzie: k_T i k_R - współczynniki skali odpowiednio temperatury i oporów.