IMAG0090 (2)

Potencjały. Źródła I promieniowanie fal

122

Elektryczny potencjał Hertza wykorzystuje się w teorii falowodów do analizy fal typu E, podobnie jak to ma miejsce z zastosowaniem magnetycznego potencjału Hertza do analizy fal typu H.

6.7

OBLICZANIE PÓL W SĄSIEDZTWIE DIPOLA HERTZA

W przykładzie rozwiązanym w p. 6.2 rozwalaliśmy dipol elektrostatyczny złożony z dwóch równych co do modułu ładunków różnoimiennych odległych od siebie o I. Obliczyliśmy pole elektryczne w punktach przestrzeni otaczającej dipol odległych od dipola o r l. Załóżmy teraz, że ładunki zmieniają się w czasie harmonicznie i są połączone cienkim przewodem o długości /. Jeżeli

q ss q₀ e^J“‘    (6/61)

to w przewodzie popłynie prąd

J «= -g₀ jo**** = -jfo c^,wt    (6/62)

Załóżmy dodatkowo, że jest spełniony warunek

l< A    (6/63)

przy czym A — długość fali o pulsacji co w przestrzeni otaczającej dipol.

Opisany układ ładunków zmiennych w czasie jest nazywany dipolem Hertza.

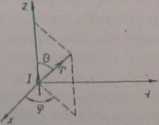
6/3

Antena krótka

Załóżmy, że dipol Hertza jest umieszczony w próżni, w środku układu współrzędnych (rys. 6/3). W.rozważanym przypadku dogodnie jest zastosować układ sferyczny. Podstawienie wzoru (6/62) do (6/39) daje

ii(r) = -i,j _(f,cosfl-f,sin0)i^-e^l<“^,-''>    (6/64)

⁷    4 nr    4 nr

Po znalezieniu potencjału wektorowego A poszukujemy wzoru określającego

pole magnetyczne w danej przestrzeni. Skorzystamy do tego celu z zależności

H =— B fc    (6/65)

P P

Do wyrażenia (6/65) należy podstawić wzór (6/64) uwzględniając zależność (D2/24) opisującą rotację we współrzędnych sferycznych. W rozważanym przypadku potencjał wektorowy nie ma składowej w kierunku oraz nie wykazuje zmian w kierunku i , co powoduje, że pole magnetyczne ma tylko jedną składową

(6/66)

" ^{= i}’^f^sin0(T