3582317793

PRZYKŁADY t- .^OGNOZ

ZADANIE 1

W okresie 15 tygodni zanotowano w magazynie zaopatrzenia następujące liczby samochodów dostarczających niezbędne do produkcji surowce :

Tydzień	Liczba samochodów
1	84
2	81
3	89
4	90
5	99
6	106
7	127
a	117
9	127
10	103
11	96
12	96
13	S6
14	101
15	109

ĆWICZENIE nr 2

POTRZEBY MATERIAŁOWE - ilościowe metody prognozowania

Określić przy wykorzystaniu metody naiwnej liczbę samochodów obsługiwanych w terminalu

1. Zgodnie z modelem dla metody naiwnej prognozę można sporządzić dla okresu

Tydzień	Rzeczywista liczba samochodów (D^	Prognoza F{ltr1) na podstawie danych z ostatniego okresu	Błąd prognozy
1	84	-	-
2	81	&V	-I
3	89		9
4	90	8 9	4
5	99	90	9
6	106	99	?
7	127	-106	a-i
8	117	IZ/*	-40
9	127	44?	40
10	103	41?	-T.H
11	96	409
12	96	96	0
13	86	96	-40
14	101		4S
15	109	404	s
16	-	4 0 3>

ZADANIE 2

Dla danych jak w ZADANIU 1 opracować prognozę dla 16 tygodnia opartą na średniej ruchomej wartości danych dla danych z a) dwóch, b) czterech okresów

t 'bfa F_1&-- łoi

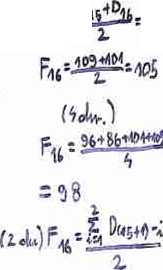
Tytóeń	Rzeczywista liczba samochodów	PROGNOZA (średnia z 2 okresów)	PROGNOZA (średnia z 4 okresów)
1	84	-	-
2	81	-	-
3	89	82,5	-
4	90	35	-
5	99	m _____
6	106	ca sT' Ln	89, ?S
7	127,	'101,5	96
fl	117!	416-5	405,5
9	127	47.2,0	442,25
10	103	412,0	449/25
U	96	AAŚ	448.5
12	96	99,5	440,95
13	86	34	4D5.5
14	101	94	9«2S
15	109	_33/5	94.95
18	-	405	98
średnia	4M	Ar, A	4I?S
wartość min	S4	83	86
wartość mar	Al ?	42.1	_115_

⁴ ^uO

R,₀ -

6c(jualtftV<£,