3582324394

1)    wstali 1:100000,

2)    w stali 1:50 000,

3)    w stali 1:25 000.

4)    sekcji podziałowej.

49.    Wstępne analizy doktadnościorwo majp na celu:

1)    tylko ustalenie wymaganej dokładno* ci pomiarów w sieci,

2)    tylko ustalenie optymalnej konstrukcji sieci,

3)    ustalenie wymaganej Hnkiiufantei pomiarów w sieci i ustalenie optymalnej konstrukcji sieci.

4)    wyłącznie odrzucenie obserwacji odstalopących.

50.    Kompensatory w instrumentach geodezyjnych słnźą do:

]) wyznaczania błędu Indeksu,

2)    eliminacji grubych błędów,

3)    wyznaczenia i stabilizacji kierunku pionu tub poziomu,

4)    pomiaru odległo* cL

Modele Statywtynme- Bachanek Wyrównawczy

1. Który zapis n»cieizowy jest pojrawny:

1) A B = C

m.n «.* tnj

2) A B = C

m.n njc m,k

3) A B = C

m.n kji    m.n

4) A B = C

m.n oiA mjt

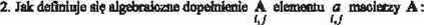
U

M - minor olenmjtu a

U

1) A =M

U ‘J

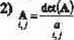
3> _A=(-ir'M

u u

4) A = a M

3. Jak definiuje się, ddeid macśeczy A :

1)    d=Jł(A)-m

2)    d =J?{a}-«

4) d =nnn{B,Bł}-/l{A}

3)    d=n-R(A)

4. Macierz ortogonalna musi spełniać warunek:

1) AA^t =A^rA=E    B-m»oicrzjednostkowa

2) AA^r =E    B-macierz jednostkowa

3)    AA^r = A^tA = D D - macien diagonalna

4)    AA^r =D    D • macierz diagonalna

5. ZakJadąjęc,żeistnieje jednoznaczny rozkład macierzy A na czynniki trbjkąme A = H⁷ X G, można wyznaczyć odwrotność maciazy A według zależności:

1)    A"' =(a^r)'¹ xG^_1

2)    A^-1 =G^_1 x(h^t^‘

3)    A^-1 =Gx(a^,')'‘

4)    A"¹ =(h^t)xG~^!

6. Dane są dwie macktzo kwadratowe stopnia 8. Macierz A jest obarczona defektom d =3, natomiast mącisz B - defektem d - 4. Iloczyn tych macierzy obarczony będzie defektem większym niż:

1)1

2) 3

3) 4

4) 7

7. Macierz modalna jeat to macietz utworzona na podstawie:

8. fałd warunek mtutzę spełniać zdarzenia niezależne:

1)    Ąa-b)=Ąa)Ąb\a)

2)    Ąa b)=Ąb)Ąa\b)

3)    ĄAB)=Ąa)ĄB)

4)    Ąa ■ a)=Ąa}± Ąb) -Ąaub)

9.    Kita: * charakterystyk liczbowych jednowymiarowej zmiennej losowej rą miarę roazuls jej wartości:

1) wartość przeciętna E{X}

2} wariancja V{X}

3)    współczynnik asyruBtrii

4)    współczynnik skupienia

10.    Jak wyraża się funkcja prawdopodobieństwa w rozkładzie dwumianowym:

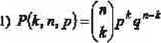
2) Ąk,n,p)=nkp^kq*-^k

3)    Ąk,n,p) JjL^l_p^kr^k

Al

4)    Ąk,n,p)=j^p^kq‘^r'ⁱ

11. Funkga gęstości rozkładu normalnego posiada maksimum dla;

1)    x=o

2)    X = (i