3582460705

M-4

WAHADŁO SPRĘŻYNOWE

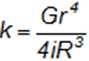
WYKONANIE ĆWICZENIA

A. Sprawdzenie prawa izochronizmu drgań wahadła sprężynowego.

1.    .Zawieszamy masę 4M na sprężynie. Rozciągamy sprężynę o x=1cm i puszczamy swobodnie. Stoperem mierzymy czas N=20 wahnieri. Pomiar powtarzamy trzykrotnie.

2. Zwiększamy amplitudę drgań o 1cm, aż do 6cm i wykonujemy pomiary jak w punkcie 1.

3. Za pomocą wagi laboratoryjnej wyznaczamy masę M.

B. Badanie zależności okresu wahań od masy M zawieszonej na sprężynie i masy sprężyny m.

1.    Na sprężynie zawieszamy kolejno masy M, 2M, 3M,... i wychylamy każdą z nich o x=2cm. Podobnie jak w punkcie A mierzymy czas N=20 wahnieri. Pomiar powtarzamy trzykrotnie dla każdej masy.

2.    Za pomocą wagi laboratoryjnej wyznaczamy masę sprężyny m oraz odważników M

OPRACOWANIE ĆWICZENIA POWINNO ZAWIERAĆ:

1.    Zestawienie tabelaryczne wyników

pomiarów okresów i mas odważników (M) i sprężyny (m) oraz błędów pomiarowych.

2.    Wykresy zależnści:

T = f(x):

lnM + ±m

T = 2.t J-; n =1,2,3,.

3.    Testujemy prawo izochronizmu wahań: Okres drgań nie zależy od amplitudy drgań dla małych wychyleń (x«/)

T=f(x)=a;

gdzie a stały parametr.

4.    Testujemy zależność okresu wahań od masy odważników M i masy sprężyny m. Wyznaczamy współczynnik sprężystości sprężyny k.

T = a,jM^ gdzie M_x =nM + -m\ n= 1,2,...I

3

a - "fitowany parametr” a = 2^/^; k - współczynnik sprężystości sprężyny.

Wyznaczanie współczynnika sprężystości

Z rozważań teoretycznych dotyczących rozciągania sprężyny wynika, że stałą sprężyny k można obliczyć ze związku gdzie

6 - 'współczynnik sprężystości postaciowej (zwany modułem sprężystości postaciowej) 6 = 33,385 10⁹ N/m² (stal), r- promień drutu,

/ - liczba czynnych zwojów sprężyny,

R - promień nawinięcia sprężyny.

Oblicz stałą k i porównaj z wartością otrzymaną z aproksymacji wyników pomiarów

Dla punktu 3. i 4. Podaj poziom ufności 1-a weryfikowanych hipotez, wartość statystyki testowej 'Ć. liczbę stopni swobody ndf. wartości parametrów a. k oraz biedy pomiarowe Aa. Ak Nanieś fitowane zależności na wykresy

5 Własne wnioski.