3582461702

Zadania z matematyki na egzamin wstępny na studia II stopnia

Wydział MDM UW ostatnio poprawki: 19 maja 2010

Spis treści

Wstęp    1

1    Analiza Matematyczna i Równania Różniczkowe    1

2    Geometria z Algebrą Liniową i Algebra    9

3    Topologia z elementami Teorii Mnogości    13

4    Rachunek Prawdopodobieństwa z elementami Statystyki    15

5    Przykłady rozwiązanych zadań    19

Wstęp

Egzamin trwa co najmniej 210 minut i składa się z śedmiu zadań wybranych z poniższego zestawu: trzech z części pierwszej, dwóch z części drugiej, jednego z części trzeciej i jednego z części czwartej. Zadania wybier.uie są tak, aby tematyka objętego nimi materiału była możliwie najszersza. Podczas egzaminu nie wolno posługiwać się telefonami komórkowymi, kalkulatorami, laptopami, ]>aliutopami itp. Wszystkie odpowiedzi należy uzasadnić.

Rozwiązania każdego zadania punktowane są w skali 0-10. Wynik każdegp zdającego jest sumą zdobytych przezeń punktów. Nie są wystawiane oceny w tradycyjnej skali, a na życzenie kandydata wydaje się tylko zaświadczenia o liezUe zdobytych punktów. Ranking kandydatów tworzony j<st w kolejności uzyskanych wyników.

1 Analiza Matematyczna i Równania Różniczkowe

1.    Podać przykład funkcji /: R —* R, która nie* jest ciągła w żadnym punkcie swojej dziedziny, oraz przykład takiej funkcji /: R —* R, która jest ciągła w eloklaelnie jednym punkcie swojej dziedziny.

2. Udowodnić, że jeśli funta ja /: R —* IR jest wielomian en i nieparzystego stopnia, to dla każdej liczby y € R istnieje taka liczba x € R, że f(x) = y. Wykazać, że* nie jest to prawdą ella żadnego wielomianu stopnia parzystego.

3.    Podać przykład takiej funkcji /: R —* R, że* ella każdej liezln- 6 > 0 zachodzi inkluzja

4.    Znaleźć wszystkie punkty ciągłości funkcji /: R² —► R,

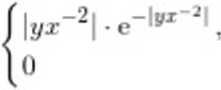
ella x 0: ella x — 0.

5.    Udowodnić, że* jeśli funkc ja /: [0. +oo) — R jest ciągła i ma asymptotę w +oc, czyli gdy istnieją takie* liezln' a.h € R, że lim_z—oo (/(x) — (eur -f 6)) = 0, to / jest jednostajnie ciągła.

6.    Znaleźć pochodną funkc ji f(x) = (2 + sinx)^x, x € R.

1