2740389176

14 Piotr Aliawdin, Krystyna Urbańska

max₇ $(S, K_n j eJ)<0, j eJ,    (3.5)

gdzie Kj, j e J, oznacza zbiór wektorów złożonych ze stałych parametrów, podobnych jak w PP. 2.1 i 2.2.

Problem (3.1) - (3.3) jest zagadnieniem programowania liniowego natomiast (3.1), (3.4), (3.5) dotyczy zagadnienia programowania nieliniowego dla konstrukcji zespolonych w stanie nośności granicznej z poślizgiem.

4. ANALIZA NUMERYCZNA BELKI ZESPOLONEJ

Obliczenia numeryczne wykonano w środowisku systemu Abaąus/Standard [1]. Przeprowadzono je dla belki zespolonej stalowo-betonowej, swobodnie podpartej o długości 5 m, obciążonej w środku rozpiętości siłą skupioną F. Płyta betonowa o grubości 12 cm i szerokości 80 cm połączona jest z belką stalową, którą stanowi dwuteownik PN-300 (rys.8).

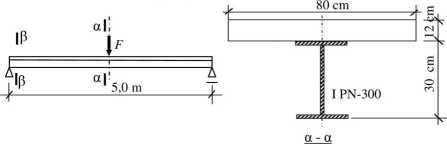
Rys. 8. Schemat obciążenia i przekrój poprzeczny analizowanej belki

Dla elementów składowych belki zespolonej przyjęto następujące dane materiałowe: dla betonu ściskanego [14] moduł sprężystości betonu E_c= 30745 MPa; wytrzymałość na ściskanie f_c=32,37 MPa; odkształcenie przy ściskaniu odpowiadające maksymalnej wytrzymałości na ściskanie e_C|=0,0022, dla stali, z której zostały wykonane dwuteowniki typu PN-300, granica plastyczności wynosi 273,0 MPa.

W obliczeniach numerycznych przyjęto następujące modele materiałowe:

a)    dla betonu - z wzmocnieniem plastycznym,

b) dla stali - idealnie plastyczny.

Płytę betonową w analizie MES zamodelowano za pomocą ośmiowęzło-wych elementów bryłowych (C3D8R), belkę stalową zaś za pomocą elementów płytowych (S4R).