2257240462

Zadanie 29. (2 pkt)

Na rysunku przedstawiono fragment wykresu funkcji/ który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem y = — dla każdej liczby rzeczywistej -v =± 0

1

y = -

X

i    i

y = - * = [2,-1] =>/(*) =

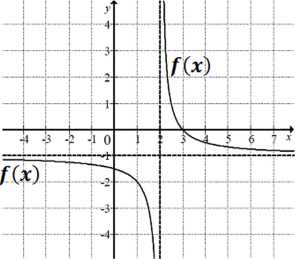
a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości

funkcji/sa. większe od 0.

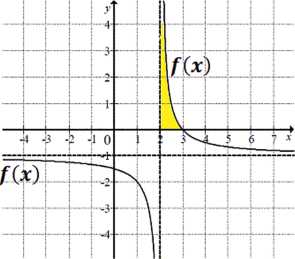
/(x) > 0 <=>

-x + 3

> 0

x - 2

D:X e R\{2}

(-x + 3)(x - 2) > 0 /(x) > 0 <=> x e (2,3)

b) Podaj miejsce zerowe funkcji g określonej wzorem g(x) = f(x - 3).

/(*) = /(*) /(*) ^: /(*) /(*)

+

l(x - 2)

2 x- 2 l(x — 2)

x - 2 - x + 2

x - 2 -x 3

g(x) = f(x - 3) i

g(x)

g(x) = O <=>

-x + 6

g (*)

x - 2 1

x - 5 5*o x * 5

g(x) =

g(x) = g(x) = g(x) =

x - 5 x - 5 1 — (x — 5)

x - 5 1 - x + 5

x - 5 -x + 6 x - 5

D: XER\{-5}

-x + 6 = 0 -x = -6 x = 6 e D

g(x) = 0 <=> x = 6

Minor