3469513952

FIGURY PŁASKIE

TRÓJKĄT

środek okręgu opisanego wyznaczają symolmlne boków, śmdok okręgu wpisanego wyznaczają dwusieczno kątów Nie ma środka sym

A równoramienny: ma 1 oś sym.. kąty przy podstawie równo, wysokość dzieli podstawę na potowę.

r =

\

— a

2

h

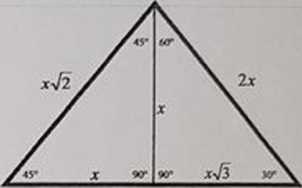
TRÓJKĄT równoboczny

Każda wysokość jest dwusieczną kąta. symetnalną boku. środkową trójkąta. Wysokości przecinają się w jednym punkcie wyznaczając środek okręgu wpisanego i opisanego. Punkt ten dzieli każdą wysokość na odcinki w stosunku 1:2 (długości r = 1/3 h i R= 2/3 h).

Ma 3 osie sym. Jest figurą FOREMNĄ.

KWADRAT

Przekątne są równe, przecinają się pod kątem prostym, w połowie długości, wyznaczając środek okręgu wpisanego i opisanego. Jest rombem i deltoidem. Ma 4 osie i środek sym. Jest figurą FOREMNĄ.

PROSTOKĄT

Przekątno są równo, przocinają się w połowie wyznaczając środek okręgu opisanego.

Ma 2 osie sym. i środek sym.

RÓWNOLEGŁOBOK

Przekątne przecinają się w połowie długości. Nie ma osi sym.. ma środek sym.

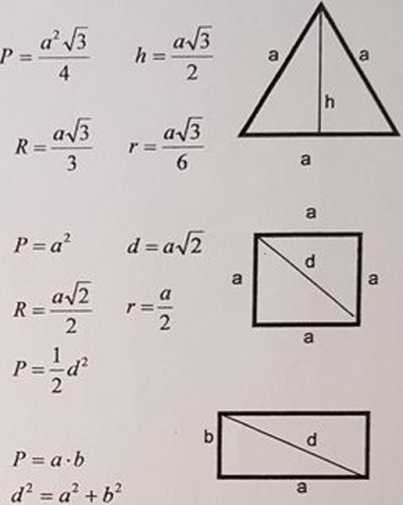
P = ah

ROMB

Przekątne w rombie są dwusiecznymi kątów, przecinają się w pokwrie swej długości, pod kątem prostym.

Jest deltoidem. Ma 2 osie i środek sym.

P = ah

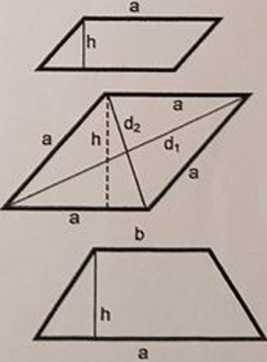
TRAPEZ

W trapezie równoramiennym są równo ramiona i kąty przy toj samej podstawio. Nie ma środka sym.

Suma kątów pizy ramieniu 180^c

_p_(a + b)h 2