79571848

Zestawy zadań maturalnych

Zestawy zadań oznaczonych literą „M" po każdym dziale: Zadania testowe,Zadania krótkiej odpowiedzi, Zadania rozszerzonej odpowiedzi ułatwiają kształcenie umiejętności rozwiązywania zadań typu maturalnego. Do każdego zadania w tych zestawach przypisana jest punktacja, która daje wyobrażenie o stopniu ich trudności.

1	\
o	•\			X

Powtórzenie przed maturą

W klasie 4 obszerne powtórzenie całego materiału szkoły ponadpodstawowej pozwala na ugruntowanie wiedzy i skontrolowanie stopnia opanowania umiejętności sprawdzanych na maturze.

Sposób na zadanie

Przykład 1

Prootn u ■ ox+b przechodzi przez punkty P i Q. Współczynnik a jest ujemny. *dy:

c./>(-|.-J).q(§.$),

b. p(J.-J). <?(?..)•    <?«,})•

Ab>- wskazać poprawny odpowiedź, motany postąpić na jeden z poniższych sposobów:

•    obliczyć współczynniki kierunkowe prostych w każdym z przypadków A. B. Ci D.

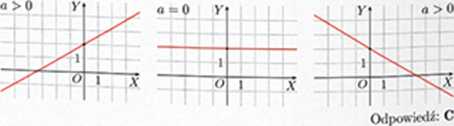
•    zaznaczyć punkty Pi<?w ukłiMizie współrzędnych i zobaczyć, w którym przypadku prosta PQ jest wy-kresem funkcji malejącej (na rysunku obok przedstawiono prostij PQ dla przypadku D).

•    zauważyć, żc w przypadku D: zp < Xq (gdyż < 5) oraz yp> Vq (sdyż

•    > |). zatem prosta PQ jest wykresem funkcji malejącej, czyli a < 0.

Od|X>wicdź: D

Przykład 2

Która |»ara punktów nic należy do prostej y - oz -t- 2 dla żadnej wartości współczynnika a?

A.    (-8. -5). (8.9)    C. (-8. -6). (4. -2)

B.    (-9,6). (9.-2)    D. (-10.4). (5,1)

Aby wskazać poprawin) odpowiedź, możemy postąpić na jeden z poniższych sposobów:

•    sprawdzić współliiiiowcść podanych punktów’ z punktem (0.2) w każdym

•    iwzypadków A. B. C i D.

•    zauważyć, że prosta y = ax + 2 nic może przechodzić jednocześnie przez punkty naleięoc do III i IV ćwiartki układu współrzędnych (patrz rysimki). a takie punkty podano w przy pul ku C.

Zadania testowe

Rozwiąż zadania i zapisz odpowiedzi w zeszycie. W każdym zadaniu tylko jedna od|>owiedź jest prawidłowa.

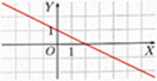
1.    Na rysunku ol>ok przedstawiono wykres ftuik-cji liniowej o wzorze:

A. /(x)-§x + 2.    C. /(x) = jz + 1.

B.    /(x) ■ -Jx + 2.    D./(x)»-$x+l.

2.    Przez któri) ćwiartkę układu współ rzędnych nic przechodzi wykres funkcji /<x)--*x-4?

A. I    B.    II    C. III    D. IV

3.    Miejsce zerowe    funkcji /(x) -    y/lz + 4 jest równe:

A. -2V5. B.    C. 2.    D. 2\/2.

4.    Prosta przechodząca przez punkt (-1.6) i przecinająca oś O A' w punkcie o odciętej I przecina oś OY w punkric:

A. (0.3).    B.    (0, j),    C. (0.-3).    D. (0.-6).

5.    Punkt A(2A, 7)    należy do wykresu    funkcji /(x) = 2x + I dla:

A. *

6.    Do w

A* (-

7.    Pro»t A. tri

8.    Dwa

prost

w pn obok.

A.    20

B.    24

9.    Kłóri

wspó

A.    (4.1). (-4. -3)    C. (-3. -2). (-1.3)

B. (-3.-10). (I.—2)    D. (1.3). (3.-3)

Sposób na zadanie

W podręczniku na stronach Sposób na zadanie pokazano kilka metod rozwiązania tego samego zadania zamkniętego. To pozwoli uczniom porównać je i zapamiętać, że każde zadanie można rozwiązać różnymi sposobami.