20356

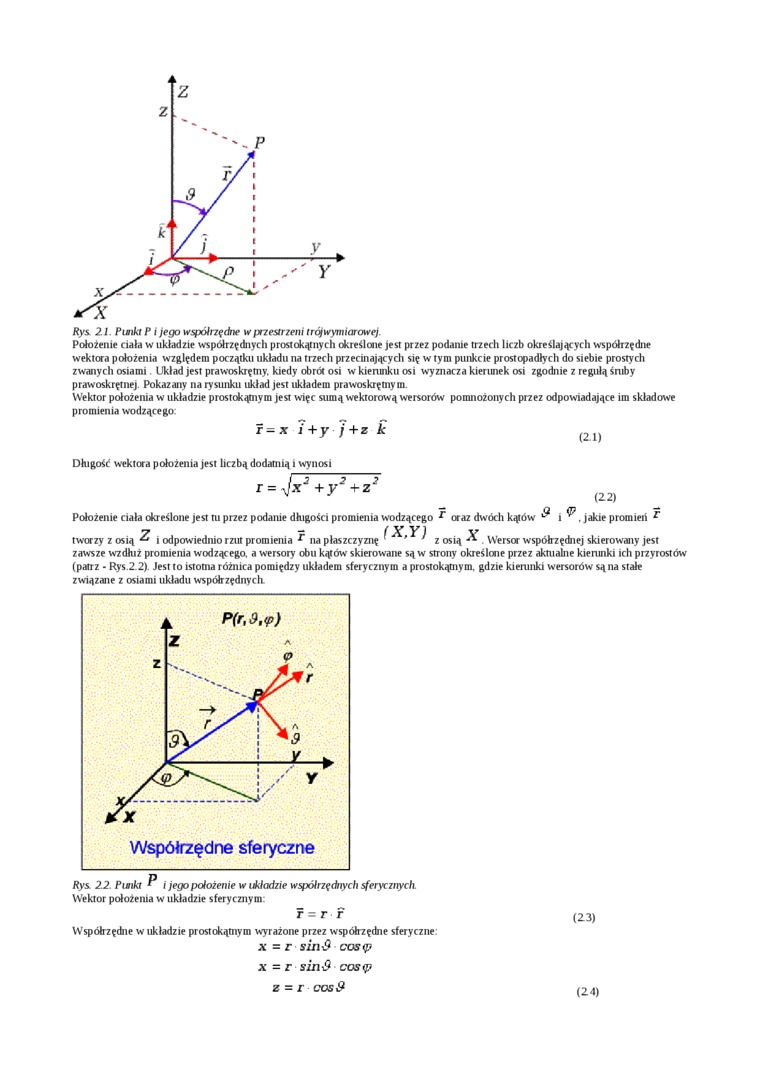
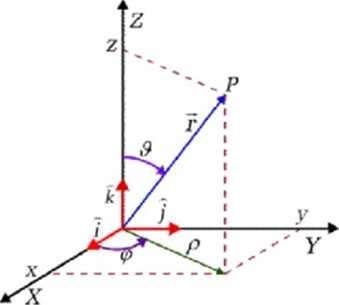
Rys 2.1. Pimkt P i jego współrzędne w przestrzeni trójwymiarowej.

Położenie ciała w układzie współrzędnych prostokątny cli określone jest przez podanie trzech liczb określaj ącycli współrzędne wektora położenia względem początku układu na trzech przecinających się w tym punkcie prostopadłych do siebie prostych zwanych osiami. Układ jest prawoskrętny, kiedy obrót osi w kierunku osi wyznacza kierunek osi zgodnie z regułą śniby prawoskrętnej. Pokazany na rysunku układ jest układem prawoskręmym.

Wektor położenia w układzie prostokątnym jest więc sumą wektorową wersorów pomnożonych przez odpowiadające im składowe promienia wodzącego:

f=x ?+y j+z k

Długość¹ wektora położenia jest liczbą dodanuą i wynosi

} 2    2 J

(2.2)

r = _A/x +y +z

Położenie ciała określone jest tu przez podanie długości promienia wodzącego ^r oraz dwóch kątów & i ^. jakie promieti ^r

tworzy z osią ^ i odpowiednio rzut promienia ^r na płaszczyznę ^    _z osią ^ Werscr współrzędnej skierowany jest

zawsze wzdhiż promienia wodzącego, a wersory obu kątów skierowane są w strony określone przez akmabie kierunki ich przyrostów (patrz - Rys.2.2). Jest to istotna różnica pomiędzy układem sferycznym a prostokątnym, gdzie kierunki wersorów są na stałe związane z osiami układu współrzędnych

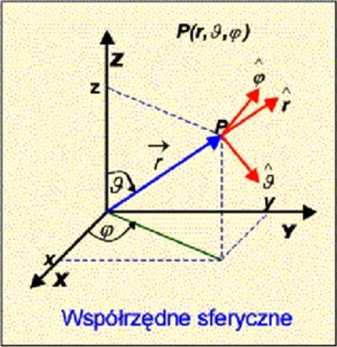
Rys 2.2 PiMikt P i jego położenie w Madzie współrzędnych sferycznych. Wektor położenia w układzie sferycznym:

(23)

(24)

r = rr

Współrzędne w układzie prostokątnym wyrażone przez współrzędne sferyczne:

x = r sin& costp x = r sin£ costj?

z = r cos&