24418

f(ccii+ 0v) = f(a(x,,x,,x₃)+ /}(y„y₂,y_s)) =

=/((<**>⁺ Py^^axi+Py₂>^ax> + Py> ))=

=(«U - *₂ ⁺ 2x>)+P(y, - y₂ + -y> ).“(*i + *₂+^ )+

+ P(>\ + y₁ + y_i ).<*(3*, + 3*₂ + 3A-J+ p(3y, + 3y₂ + 3 y_s)) =

= <*(x,-x₂ + 2x_s,x_i + x, + x₃,3x, + 3x, + 3x_s)+ /?(>', - y₂ + 2y_s,y, + y₂ + y„3y, + 3y₂ + 3y,) <*f(^xv*₂’X₃)+Pf(y_l,y₂,y_}) = af(u)+pf(v)

Odwzorowanie f jest liniowe Definicja 2.

(A^r,AT,+,-),(y,AT,+,*) - przestrzenie wektorowe f:X-±Y jest liniowe

Jądrem odwzorowania liniowego nazywamy ogół takich wektorów z przestrzeni X, których wartość jest wektorem zerowym przestrzeni Y

Kerf:={?eX:/(3F)=0_v}

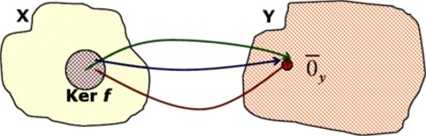
Obrazem odwzorowania f (przedwdziedziną, zbiorem wartości) nazywamy zbiór

Im / := {y e Y : 3_TeA.: y = /(*)}

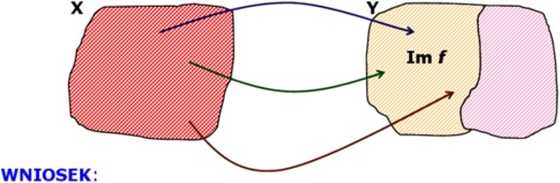
Ker/= /-'[{()}] Im/ = {/(x):xe*}

Wykład dr Magdaleny Sękowskiej strona 2 z 5 Część 5 -Odwzorowania liniowe