2601

W tablicy korelacyjnej zawarte są dwa rodzaje rozkładów: brzegowe i warunkowe. Rozkład brzegowy prezentuje strukturę wartości jednej zmiennej (x lub y) bez względu na kształtowanie się wartości drugiej zmiennej. Z tego wynika, że w tablicy korelacyjnej są dwa rozkłady brzegowe. Rozkład brzegowy zmiennej X tworzy pierwsza i ostatnia kolumna tablicy, natomiast rozkład brzegowy zmiennej Y - pierwszy i ostatni wiersz.

Rozkład warunkowy prezentuje strukturę wartości jednej zmiennej (x lub y) pod warunkiem, że druga zmienna przyjęła określoną wartość.

Rozkład warunkowy zmiennej x zapisujemy następująco: x/y = y,;

Rozkład warunkowy zmiennej y zapisujemy następująco: y/x = x,.

Rozkładów warunkowych zmiennej x jest więc w tablicy tyle, ile wariantów zmiennej Y i na odwrót.

Rozkłady brzegowe i warunkowe mogą być scharakteryzowane pewnymi sumarycznymi wielkościami. Szczególnie użytecznymi miarami są średnia arytmetyczna i wariancja (lub odchylenie standardowe).

Średnie arytmetyczne z rozkładów brzegowych oblicza się następująco:

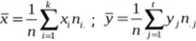
Średnie arytmetyczne rozkładów warunkowych oblicza się następująco:

*=—E*.ⁿ« ;

ⁿj i-i    ⁿi i

Jeżeli ze wzrostem (spadkiem) konkretnych wartości jednej zmiennej obserwuje się wzrost (spadek) warunkowych średnich drugiej zmiennej, to fakt ten świadczy o istnieniu korelacji dodatniej między zmiennymi. Przeciwny kierunek tych zmian informuje o istnieniu korelacji ujemnej.

Na podstawie tablicy korelacyjnej można również stwierdzić, czy związek między zmiennymi X i Y jest liniowy.

Liniowość związku stwierdza się na podstawie różnicy między średnimi wariantami danej zmiennej, obliczonymi dla konkretnych wariantów drugiej zmiennej. Związek jest liniowy, jeżeli różnice między średnimi są takie same, tzn.:

-x₂ =... = x_r

y₂ -Pi =x₃ -y₂ =-=y* -y*-.

Wariancje poszczególnych rozkładów cechy x oblicza się następująco:

ⁿ

⁼    ~^x> (j = 1,2.....r)