Image 81

W powyższej równości zawarte są dwa aspekty procesu produkcji. Marginalna stopa technicznej substytucji informuje producenta o możliwościach technicznych jakie ma do dyspozycji, natomiast relatywne ceny czynników są informacją rynkową, którą producent musi wziąć pod uwagę. Jeżeli MSTS i w/r nie są sobie równe, wówczas producent może polepszyć swoją sytuację zmieniając kombinacje nakładu czynników.

Przyjmijmy, że ceny czynnika pracy i kapitału są równe - stąd w/r = 1, natomiast MSTS wynosi 2 (zwiększając nakład czynnika pracy o dodatkową 1 jednostkę zmniejszamy nakład kapitału o 2 jednostki). Producent posiada następującą możliwość: zmniejszając nakład kapitału o 2 jednostki może dodać do produkcji 2 jednostki czynnika pracy przy zachowaniu tego samego kosztu całkowitego. Oznacza to, że przy tym samym koszcie producent może zwiększyć produkcję (przejść na wyższą izokwantę) dodając więcej czynnika pracy i równocześnie redukując nakład czynnika kapitału. Tak więc, jeżeli PM_L/PM_K > w/r (punkt A na wykresie 77) można osiągnąć większą produkcję przy tym samym koszcie zwiększając ilość czynnika pracy i zmniejszając ilość kapitału. W przypadku kiedy PM_L/PM_K < w/r (punkt B na wykresie 77) można zwiększyć produkcję zwiększając ilość czynnika kapitału i ograniczając ilość czynnika pracy. Tylko w punkcie równowagi nie jest możliwe osiąganie większej produkcji przy pomocy zastępowania jednego czynnika drugim, przy zachowaniu niezmiennego wydatku (kosztu) całkowitego na zakup czynników.

Optimum produkcji można rozpatrzyć z punktu widzenia zasady najmniejszego kosztu. Przekształcając warunek równowagi PM_L/PM_K = w/r otrzymujemy:

PM_l _ PM_k w    r

W punkcie równowagi produkcji stosunek produktu marginalnego pracy do ceny czynnika pracy jest równy stosunkowi produktu marginalnego kapitału do ceny czynnika kapitału. Oznacza to, że równowaga zachodzi wówczas, kiedy ostatnia złotówka wydana na zakup czynnika pracy daje dodatkowo taką samą wielkość produkcji, jak ostatnia złotówka wydana na zakup czynnika kapitału. Taka kombinacja nakładów czynnika pracy i kapitału jest najmniej kosztowna.

W celu wyjaśnienia powyższej zasady przyjmijmy, że PM_l = 20 (1 dodatkowa jednostka pracy daje 20 dodatkowych jednostek produkcji). Jeżeli w = 10, wtedy PM_l/w = 20/10 = 2, co oznacza, że jeśli 1 dodatkowa jednostka pracy kosztuje 10 zł i wytwarza 20 dodatkowych jednostek produktu, wówczas ostatnia złotówka wydatkowana na czynnik pracy daje 2 jednostki dodatkowe produktu. Podobne rozumowanie można przeprowadzić w odniesieniu do czynnika kapitału.

Sytuacja, w której PM_L/w > PMJr oznacza, że z ostatniej złotówki wydanej na czynnik pracy otrzymujemy więcej dodatkowego produktu (np. 2 jednostki) aniżeli z ostatniej złotówki wydanej na czynnik kapitału (np. 1 jednostkę produktu). Producent nie osiąga maksymalnej produkcji z danej wielkości wydatku całkowitego (kosztu) na zakup czynników. Jeżeli bowiem ograniczy wydatek na kapitał

fo 1 złotówkę straci tylko 1 jednostkę produktu. Równocześnie wykorzystując tę złotówkę na zakup większej ilości czynnika pracy otrzyma 2 dodatkowe jednostki produktu (PM_L/w = 2). Przy tym samym koszcie całkowitym producent zyskuje 1 jednostkę produktu. Jeżeli PM_L/w < PM^r producent może osiągnąć z danego nakładu środków (kosztów) większą produkcję zwiększając ilość kapitału i ograniczając ilość czynnika pracy.

Przy danym koszcie całkowitym maksymalny poziom produkcji osiąga się tylko wówczas, kiedy PM_L/w = PM^r.

Należy zwrócić uwagę, że obydwa równania, tzn. PM_L/PM_K = w/r, oraz PM_L/w = PM^r wskazują jedynie na cząstkowe optima producenta. Pierwsze równanie mówi o tym, jak producent kombinuje nakłady czynników, aby zmaksymalizować produkcję przy danym koszcie całkowitym. Drugie równanie wskazuje, jak producent kombinuje nakłady czynników, aby zminimalizować koszty wytworzenia danej wielkości produkcji. Obydwa tożsame optima nie odpowiadają jednak na pytanie, przy jakich rozmiarach produkcji następuje maksymalizacja zysku producenta. Zysk powstaje jako różnica między kosztem wytworzenia i ceną sprzedaży produktu. Dlatego uzyskanie odpowiedzi na powyższe pytanie wymaga uwzględnienia analizy kosztów produkcji oraz analizy kształtowania się cen produktów. Dopiero uwzględnienie tych elementów umożliwi wyznaczenie pełnej, a nie tylko cząstkowej, równowagi producenta.

Zagadnieniem tym zajmiemy się w dalszych częściach książki.

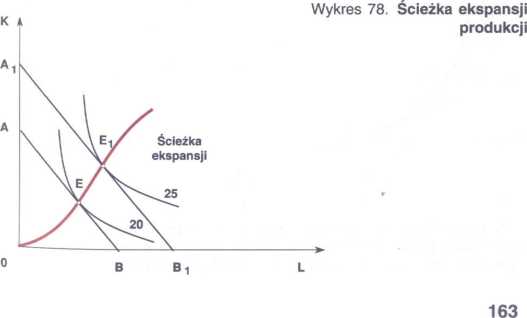
ŚCIEŻKA EKSPANSJI PRODUKCJI

Równowaga przedsiębiorstwa równoznaczna z optymalną kombinacją czynników znajduje się w punkcie styczności linii jednakowego kosztu z izokwantą produkcji. Jeżeli przedsiębiorstwo dokonuje ekspansji produkcji, wówczas osiągnięcie celu w postaci zysku maksymalnego wymaga, aby nowa kombinacja czynników była również optymalna. Przedsiębiorstwo przechodzi od jednego do następnego punktu równowagi.