Grafika Wykreślna (6)

W powyższych przykładach są dwa dachy o identycznej linii okapu, które różnią sję w częściach zaznaczonych okręgami. Z punktu widzenia konstrukcji geometrycznych - oba rozwiązania są poprawne. Z punktu widzenia przepisów budowlanych - tylko jedno. Na Rys. 18 woda spływa od kalenicy 4,8 w dół. Na Rys. 19 woda spływa na kalenicę 3,7 z góry i tworzy się bezodpływowe koryto. W tym miejscu dach będzie przeciekał. Tylko rozwiązanie z Rys. 18 jest prawidłowe.'

Jest jeszcze jeden problem, który pozornie burzy zasadę wykreślenia powtarzających się numerów przy konstruowaniu dachu. Oto przykład;

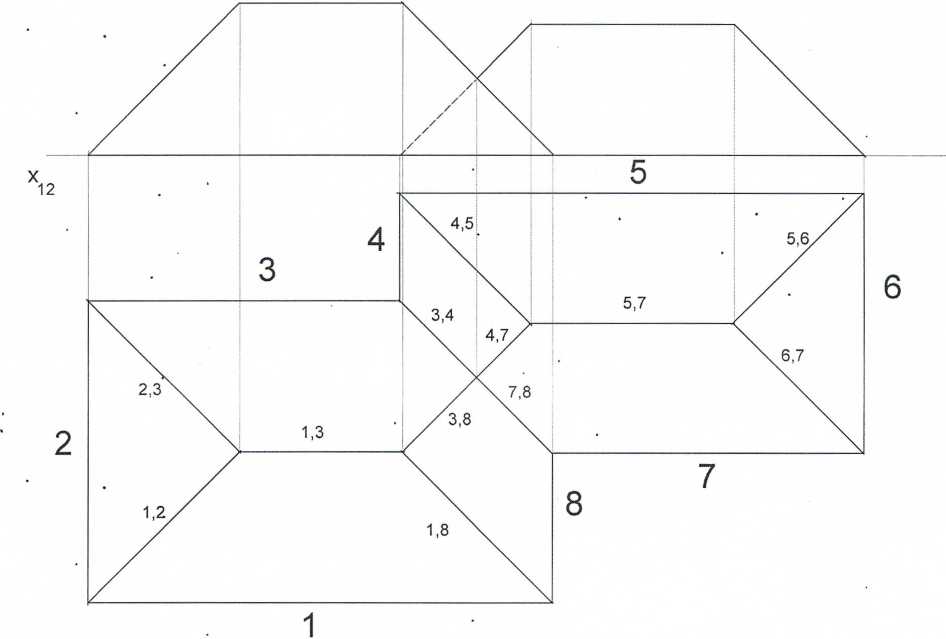
Rys. 20

W środkowej części dachu przecinają się cztery krawędzie. Zasada numerowania krawędzi jest jednak zachowana, jeśli przyjmiemy istnienie krawędzi o długości zero. Mamy wówczas na przykład: 3,4 i 3,8 - trzecia krawędź 4,8 (długości zero); 4,8 i 7,8 - następna krawędź 4,7 (tak właśnie jest).

3.3. Dachy z sąsiadem.

Sytuację projektanta dachu komplikuje fakt istnienia przylegającego do linii okapu sąsiedniego budynku, który jest wyższy od projektowanego (w przypadku niższego sąsiada - problem ma sąsiad). Przepisy bowiem nie zezwalają, aby woda z naszego dachu spływała na ścianę sąsiada, może natomiast spływać wzdłuż ściany (oczywiście - od ściany również). W celu skierowania wody wzdłuż ściany sąsiada wprowadza się dodatkowe, „wirtualne” krawędzie okapu, prostopadłe do tej ściany, na która może lecieć woda. Dla odróżnienia od rzeczywistych krawędzi, będziemy je oznaczać literami. Spotyka się trzy następujące sytuacje.

20