34543

5.4.2. Prędkość i przyśpieszenie w ruchu złożonym punktu

W celu wyprowadzenia wzorów na prędkość i pizyśpieszenie punktu M postąpimy podobnie jak podczas rozpatrywania kinematyki dowolnego punktu biyły w ruchu ogólnym, ale teraz punkt ten będzie się poruszał względem bryły. Zatem wektor wodzący r' punktu M w układzie ruchomym x\y\ z' nie będzie stały, będzie się zmieniał zarówno jego kierunek, jak i moduł:

r' = |r'|* const.    (a)

Wektor wodzący punktu M, zgodnie z rys. 5.24. jest sumą dwóch wektorów:

r = !•<>.+r'.    (5.76)

Podobnie jak w rudni ogólnym bryty (p. 5.3.2) wektor r_Q. jest wektorem łączącym początki obu układów współrzędnych. Zapiszemy go analitycznie w nieruchomym układzie współrzędnych x, y. z:

r_Q. = x₀.1+ y₀. j+ z_G. k    (5.77)

Wektor r' jest wektorem wodzącym punktu M w układzie x\y',z' . Można go wyrazić za pomocą współrzędnych w tym układzie:

r' = xT+y'J'+z'k\    (5.78)

Współrzędne tego wektora na podstawie wzoru (a) będą się zmieniać wraz z ruchem punktu M względem układu ruchomego x\ y\ z'. Można je zatem zapisać w postaci funkcji czasu, które będą równaniami ruchu względnego punktu M:

x' = x'(t). y' = /(t), z'=z'(t).    (5.79)

Prędkość punktu \1 jest pochodną wektora wodzącego (5.76) względem czasu:

v -

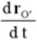
dr'

~dt~

(5.80)

Pochodna wektora r_G. jest znaną z p. 5.3.2 prędkością początku O' ruchomego układu współrzędny cli:

v

O' “

<frp-₁1 dyp. _t

dt dt ^J

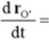
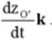
(b)

Pochodna wektora r' po zróżniczkowaniu wzoni (5.78) ma postać: