3544

Cząstki powietrza w temperaturze 273 K i pod ciśnieniem 1 atm. d = 210'⁸ cm, v = 10⁵ cm/s, n = 3-10^,9/cm³.

Wówczas średnia droga swobodna jest równa 2-10'⁵ cm (około lOOOd).

Odpowiednia częstość zderzeń wynosi 510⁹/s.

17.2 Rozkład prędkości Maxwella

Na poprzednim wykładzie omawialiśmy prędkość średnią kwadratową cząsteczek gazu. Jednak każdy gaz ma charakterystyczny rozkład prędkości, który zależy od temperatury (cząstki nie mogą mieć takich samych prędkości bo prędkości zmieniają się w wyniku zderzeń).

Clerk Maxwell podał prawo rozkładu prędkości cząsteczek, które dla gazu zawierającego N cząsteczek ma postać

(17.3)

W równaniu tym N( v)dv jest liczbą cząstek o prędkościach z przedziału od v do v + dv. T - temperatura bezwzględna, k - stała Boltzmana, m - masa cząsteczki.

Całkowitą liczbę cząsteczek można zatem obliczyć dodając (całkując) liczby dla poszczególnych różniczkowych przedziałów prędkości

N =jN(v)dt'

Na rysunku przedstawiony jest rozkład Maxwella dla dwóch różnych temperatur, gdzie -v prędkość średnia, y² - prędkość średnia kwadratowa, v_P - prędkość najbardziej prawdopodobna.

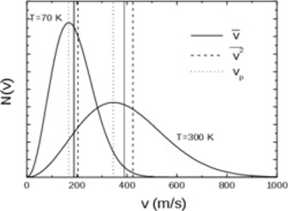
Krzywa nie jest symetryczna bo dolny limit równy jest zeru podczas gdy górny nieskończoności. Ze wzrostem temperatury rośnie prędkość średnia kwadratowa. Obszar

2