104057

Celem ćwiczenia jest wyznaczenie grubości kwarcowych płytek plasko-równołegłych, które wycięto tak, że ich oś optyczna jest równoległa do ich powierzchni czołowej (rys. 1.1). Jeśli wszystkie elementy układu ustawione są względem siebie tak jak na rysunku 1.1., to fala padająca na płytkę, rozdziela się na falę zwyczajną i nadzwyczajną o równych amplitudach, które rozchodzą się w płytce z różnymi prędkościami. W konsekwencji na wyjściu płytki pojawia się różnica faz pomiędzy tymi falami, która dana jest następującym równaniem:

(3)

A 2,rd,An(A) ^r A

gdzie ć_% jest szukaną grubością płytki.

Analizator 45°

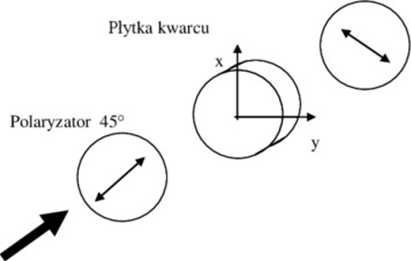
Rys. 1.1. Wzajemna orientacja polaiyzatora. analizatora i badanej płytki dwójłomnej. Oś optyczna płytki pokrywa się z osią x układu odniesienia. W takim przypadku pole elektryczne fali zwyczajnej drga wzdłuż osi y. a fali nadzwyczajnej wzdłuż osi x.

I, a wynik

Po przejściu pizez analizator fala zwyczajna i nadzwyczajna interferują ze s< interferencji można przedstawić następującym wzorem:

iu)=i„

2;rd_xAn(A) l-cos(-4-^)

(4)

Jeśli wiązkę za polaryzatorem rozłożymy na składowe spektralne przy pomocy monochromatora, to widoczne staną się wtedy tak zwane spektralne prążki interferencyjne z charakterystycznymi minimami i maksimami natężenia (rys. 1.2). Minima natężenia powstają dla tych długości fali, dla których funkcja cosinus przyjmuje wartość jeden, czyli

d*dn(A)=m A    (5)

gdzie m jest liczbą naturalna i oznacza rząd ciemnego prążka interferencyjnego. Maksima natężenia powstają dla tych długości fali, dla których spełniony jest następujący warunek:

(6)

d*dn(A)=(m+0.5)A