46610

GR.B (HE) _ —- —j
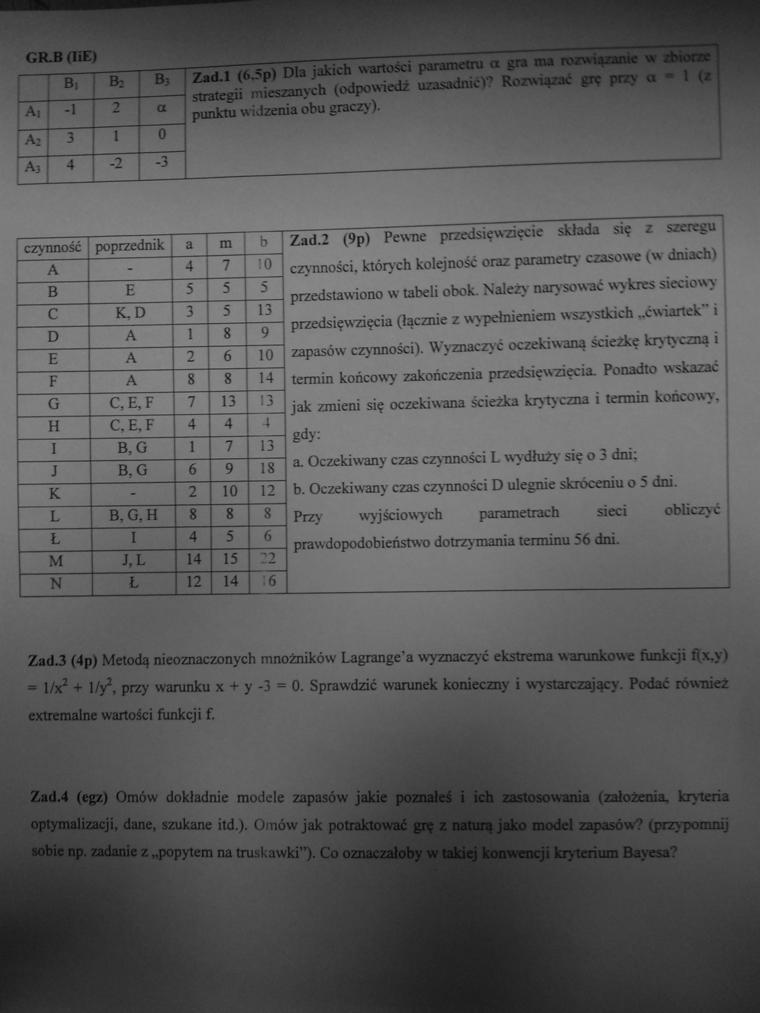
r~	B,	B:	r~Br	strategii mieszanych (odpowiedź uzasadniel” Rozwiązać grę przy a - 1 (z ! punktu widzenia obu graczy). 1
A,	•1	2	a
A:	3	1	0
Aj	4	-2	-3

czynność	poprzednik	a	m	b	Zad.2 (9p) Pewne przedsięwzięcie składa się z szeregu
A	-	4	7	!0	czynności, których kolejność oraz parametry czasowe (w dniach)
B	E	5	5	5	przedstawiono w tabeli obok. Należy narysować wykres sieciowy przedsięwzięcia (łącznie z wy pełnieniem wszystkich „ćwiartek i zapasów czynności). Wyznaczyć oczekiwaną ścieżkę krytyczną i
C	K.D	3	5	13
D	A	1	8	9
E	A	2	6	10
F	A	8	8	14	termin końcowy zakończenia przedsięwzięcia. Ponadto wskazać
G	C, E, F	7	13	13	jak zmieni się oczekiwana ścieżka krvrvczna i termin końcowy, gdy:
H	C.E.F	4	4	4
I	B, G	1	7	13
J	B. G	6	9	18	a. Oczekiwany czas czynności L wydłuży się o a dni:
K	-	2	10	12	b. Oczekiwany czas czynności D ulegnie skróceniu o 5 dni.
L	B. G.H	8	8	8	Przy wyjściowych parametrach sieci obliczyć
L	I	4	5	6	prawdopodobieństwo dotrzy mania terminu 56 dni.
M	J.L	14	15	■»2 >*- mm
N	l	12	14	:6

Zad.3 (4p) Metodą nieoznaczonych mnożników Lagrange'a wyznaczyć ekstrema warunkowe funkcji flx.y)

^{= 1/x}* ⁺ P^rz>' warunku x + y -3 = 0. Sprawdzić warunek konieczny i wystarczający. Podać również cxtremalne wartości funkcji f.

Zad.4 (cg,.) Omów dokładnie modele zapasów jakie poznali i ich zastosowania (założenia, kmeria optymalizacji, dane. szukane itd.,. Omów jak potraktować gr, z natura jako model zapasów? (przypomruj sobte np. zadanie z „popytem na truskawki”). Co oznaczałoby w takiej konwencji kryterium Bayesa’