49703

Równanie Van der Izaaka

Równanie stanu gazu doskonałego

pV = nRT

dobrze opisuje gazy rzeczywiste ale przy małych gęstościach. Pizy większych gęstościach nie można pominąć fałdu, że cząstki zajmują część objętości dostępnej dla gazu oraz że zasięg sil międzycząsteczkowych może być większy niż odległości międzycząsteczkowe.

J.D. Van der Waals wprowadził zmienione równanie stanu gazu, które uwzględnia te czynniki Jeżeli cząstki posiadają skończoną objętość to rzeczywista objętość dostępna dla cząstek jest mniejsza od objętości naczynia. "Objętość swobodna" jest mniejsza od objętości naczynia o "objętość własną" cząsteczek b. Jeżeli oznaczymy przez v objętość przypadającą na jeden mol v=V/n to otrzymamy zmodyfikowane równanie stanu gazu

p(v-b) = RT

Można również prosto uwzględnić efekt sil międzycząsteczkowych. Siły przyciągania pomiędzy « cząsteczkami (na jednostkę objętości) "po lewej" z n cząsteczkami (na jednostkę objętości) "po prawej" jest proporcjonalna do /r czyli proporcjonalna do 1/iA Siła przyciągająca znajduje swoje odzwierciedlenie w dodatkowym ciśnieniu, które zostało uwzględnione w równaniu Van der Waalsa

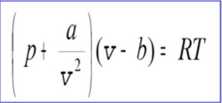
gdzie stale a i b wyznaczamy doświadczalnie. (Równanie Van der Waalsa też bywa zawodne ale nie jest znana prosta formula, która stosowałaby się do różnych gazów w różnych wantnkach).

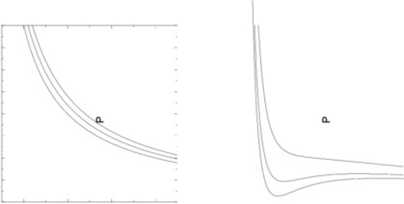
Na rysunku poniżej porównano zachowanie się gazu doskonałego (rysunek po lewej) w stałej temperaturze z gazem Van der Waalsa (po prawej).