Stadnik Krzysztof

01.03.1999r

Sprawozdanie z ćwiczenia nr 46

Temat: Wyznaczanie stałej siatki dyfrakcyjnej

Zagadnienia do samodzielnego opracowania:

1. Ruch falowy, rodzaje fal.

2. Superpozycja ciągów falowych.

3. Dyfrakcja, interferencja, siatki dyfrakcyjne.

4. Wielkości fotometryczne.

Wykonanie ćwiczenia:

1. Zestawić układ potyczny wg wskazówek prowadzącego.

2. Włączyć laser, zachowując ostrożność.

3. Ustawić siatkę dyfrakcyjną tak, aby na ekranie pojawił się ostry i dobrze widoczny obraz szczeliny.

4. Ustawić siatkę dyfrakcyjną jak najbliżej soczewki. Obserwować widoczne na ekranie prążki powstałe systematycznie po obu stronach obrazu szczeliny.

5. Zmierzyć odległość między soczewką a ekranem (y), oraz odległość między zerowym a pierwszym oprążkiem (x).

6. Pomiary powtórzyć kilka razy. Zwrócić uwagę na błąd odczytu wartości x. Aby oszacować błąd odczytu wartości y należy podczas jego pomiarów przesuwać ekran wzdłuż ławy potycznej w lewo i w prawo od położenia pierwotnego do momentu zauważenia zmiamy ostrości obrazu. Połowę przesunięcia przyjąć jako Δy.

WYNIKI POMIARÓW

λ	x	Δx	y	Δy	sin φ	d
[ nm ]	[ cm ]	[ cm ]	[ cm ]	[ cm ]	-	[cm ]
590,0	2	0.1	20	0.75	0,099	5929 10^-7
590,0	1,8	0.1	18	0.75	0,099	5929 10^-7
590,0	1,6	0.1	16	0.75	0,099	5929 10^-7
590,0	1,4	0.1	14	0.75	0,099	5929 10^-7
590,0	1,3	0.1	13	0.75	0,099	5929 10^-7
590,0	1,2	0.1	12	0.75	0,099	5929 10^-7
590,0	2	0.1	22	0.75	0,090	6516 10^-7
590,0	2,2	0.1	23	0.75	0,095	6196 10^-7
590,0	2,3	0.1	24	0.75	0,095	6184 10^-7
590,0	2,3	0.1	25	0.75	0,091	6440 10^-7

Gdzie sin φ obliczono korzystając ze wzoru :

natomiast stałą dyfrakcyjną :

Przykłady obliczeń :

Błąd Δd obliczymy korzystając ze wzoru:

Δd = λ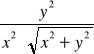
Δx + λ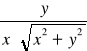
Δy =

= λ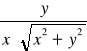
(
Δx + Δy)

Δd =

[nm]

Δd =
[nm]

Δd =
[nm]

Δd =
[nm]

Δd =
[nm]

Δd =
[nm]

Δd =
[nm]

Δd =
[nm]

Δd =
[nm]

Δd_max=856.14 [nm]

WNIOSKI

Metoda wyznaczania siatki dyfrakcyjnej polega na oświetleniu siatki dyfrakcyjnej wiązką równoległą światła monochromatycznego, która po przejściu przez siatkę ulega ugięciu. Ugięte fale pochodzące z sąsiednich szczelin nakładają się dając na ekranie maksima w przypadku spełnienia warunku: Δ=kλ. W naszym ćwiczeniu wielkość d w niektórych przypadkach ma znaczny rozrzut wynikający najprawdopodobniej z niedokładności wykonania pomiarów.

Δd = 590

Wnioski:

Metoda wyznaczania stałej siatki dyfrakcyjnej polega na oświetleniu siatki dyfrakcyjnej wiązką równoległą światła monochromatycznego, która po przejściu przez siatkę ulega ugięciu. Ugięte fale pochodzące z sąsiednich szczelin nakładają się dając na ekranie maksima w przypadku spełnienia warunku: Δ = kλ. W naszym ćwiczeniu wielkość d w niektórych przypadkach ma znaczny rozrzut wynikający najprawdopodobniej z niedokładności wykonywania pomiarów.

√x² + y²

x

sin φ =

√x² + y²

d = λ

x

√2² + 20²

2

sin φ =

= 0,099

√1,8²+18²

1,8

sin φ =

= 0,099

√1,6²+16²

1,6

sin φ =

= 0,099

√1,4²+14²

1,4

sin φ =

= 0,099

√1,3+13²

1,3

sin φ =

= 0,099

√2² + 20²

2

d = 590 10^-9

= 5929 10^-9

√1,8² + 18²

1,8

d = 590 10^-9

= 5929 10^-9[m]

√1,6² + 16²

1,6

d = 590 10^-9

= 5929 10^-9[m]

√1,4² + 14²

1,4

d = 590 10^-9

= 5929 10^-9[m]

√1,3² + 13²

1,3

d = 590 10^-9

= 5929 10^-9[m]

---