88429

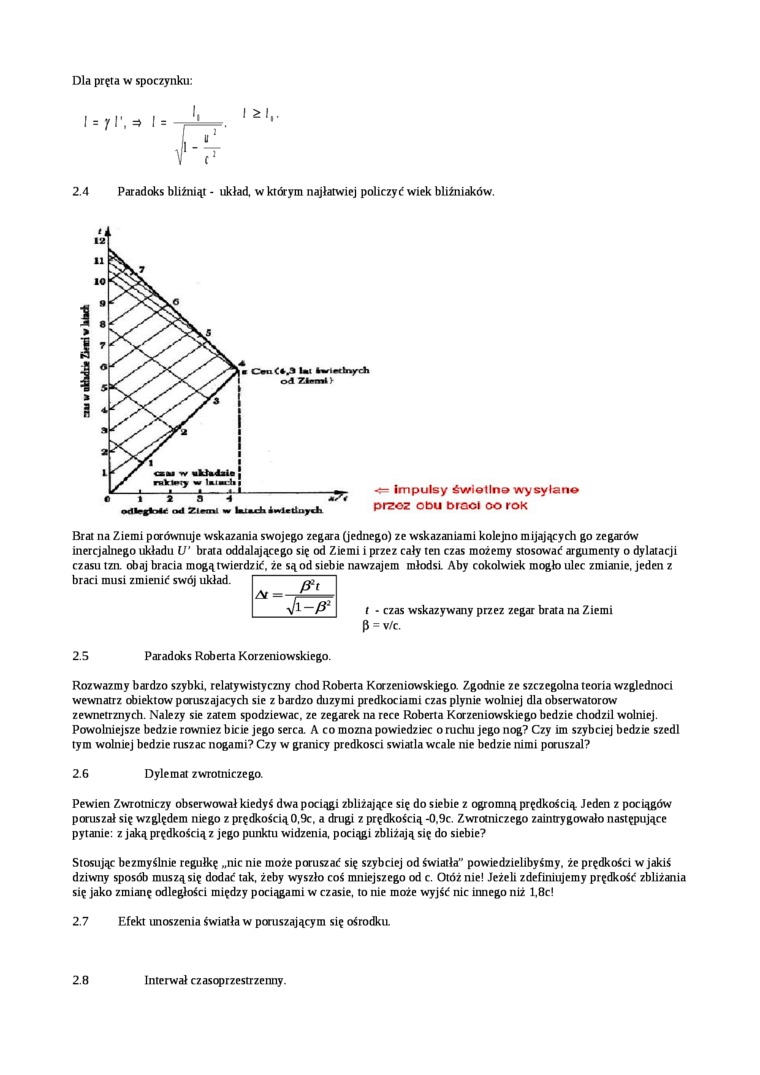
Dla pręta w spoczynku:

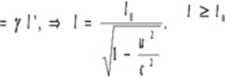
2.4 Paradoks bliźniąt - układ, w którym najłatwiej policzyć wiek bliźniaków.

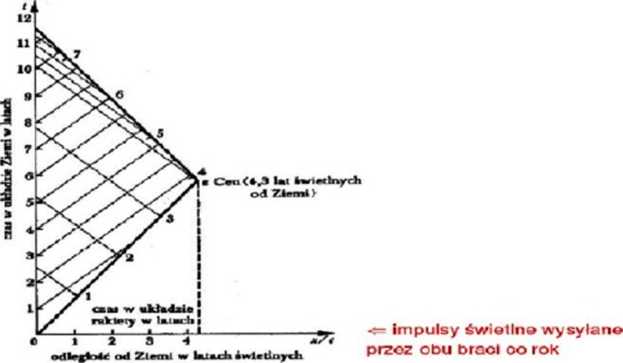
Brat na Ziemi porównuje wskazania swojego zegara (jednego) ze wskazaniami kolejno mijających go zegarów inercjalnego układu U’ brata oddalającego się od Ziemi i przez cały ten czas możemy stosować argumenty o dylatacji czasu tzn. obaj bracia mogą twierdzić, że są od siebie nawzajem młodsi. Aby cokolwiek mogło ulec zmianie, jeden z braci musi zmienić swój układ.

r - czas wskazywany przez zegar brata na Ziemi P = v/c.

2.5    Paradoks Roberta Korzeniowskiego.

Rozważmy bardzo szybki, relatywistyczny chód Roberta Korzeniowskiego. Zgodnie ze szczególna teoria wzglednoci wewnątrz obiektów poruszających sie z bardzo dużymi predkociami czas płynie wolniej dla obserwatorów zewnętrznych. Należy sie zatem spodziewać, ze zegarek na rece Roberta Korzeniowskiego bedzie chodził wolniej. Powolniejsze bedzie również bicie jego serca. A co można powiedzieć o ruchu jego nog? Czy im szybciej bedzie szedł tym wolniej bedzie ruszać nogami? Czy w granicy prędkości światła wcale nie bedzie nimi poruszał?

2.6    Dylemat zwrotniczego.

Pewien Zwrotniczy obserwował kiedyś dwa pociągi zbliżające się do siebie z ogromną prędkością Jeden z pociągów poruszał się względem niego z prędkością 0,9c, a drugi z prędkością -0,9c. Zwrotniczego zaintrygowało następujące pytanie: z jaką prędkością z jego punktu widzenia, pociągi zbliżają się do siebie?

Stosując bezmyślnie regułkę „nic nie może poruszać się szybciej od światła” powiedzielibyśmy, że prędkości w jakiś dziwny sposób muszą się dodać tak, żeby wyszło coś mniejszego od c. Otóż nie! Jeżeli zdefiniujemy prędkość zbliżania się jako zmianę odległości między pociągami w czasie, to nie może wyjść nic innego niż l,8c!

2.7    Efekt unoszenia światła w poruszającym się ośrodku.

2.8

Interwał czasoprzestrzenny.