1687289297

'349,43'

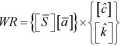
= [980 260 1 l]

= 1 468 480 zł

3547.27

137789

65959

Wykonując działania na macierzach według wzoru (12), wyliczono odchylenie standardowe szacowanej rynkowej wartości nieruchomości, czyli

a¹ (WR) = 1657,983 x [980 260 1

'31.02	-92.34	1561.85	-3856.94 '
I-I	295.00	-7277.59	10584.97
I-I	I-I	898922.81	-695651.17
/-!	I-I	I-I	1424580.04

<t‘(WR)= 1377460000 o ct(WR) = 37 114 zl

Wykorzystując kwantyla rozkładu Studenta dla 3 stopni swobody i poziomu istotności (1 — a) = 0.95, czyli /(0.95; 3) = 3,2, symetryczne przedziały ufności dla szacowanych rynkowej wartości nieruchomości przyjmuje następujące wartości:

WR = 1 468 480 ±118 765 zł

Analiza wariancji w prezentowanym przykładzie liczbowym dowodzi, że szacowana rynkowa wartość nieruchomości zawiera się w granicach przedziału ufności, którego szerokość jest na poziomie 16% jej wartości.

5. Posumowanie

Informacje z rynku nieruchomości zurbanizowanych powinny podlegać probabilistycznemu modelowaniu, które prowadzi do estymacji najbardziej prawdopodobnych jednostkowych cen elementów składowych rozważanych nieruchomości oraz wskaźników wagowych atrybutów.

W procesie estymacji tych parametrów powinna być prowadzona pełna analiza warianq'i wraz z oceną przedziałów ufności.

Określone w procesie estymacji jednostkowe wartości rynkowe gruntu oraz jednostkowe wartości części składowych gruntu można transformować na dowolną ustaloną datę. Do transformacji tej należy wykorzystywać ustalony trend zmiany cen odzielnie dla gruntu oraz oddzielnie dla części składowych gruntu, a także trzeba oszacować stopień zużycia technicznego i funkcjonalnego budynków.

15

Studia i Materiały Towarzystwa Naukowego Nieruchomości - vol. 16 nr 3 2008