3826200106

1. Wprowadzenie

przejścia procesu losowego przez liniowy system dynamiczny oraz identyfikację jego parametrów metodą najmniejszych kwadratów. Materiał do każdego ćwiczenia rozpoczyna się od obszernego wstępu teoretycznego. Następnie przedstawiony jest plan badań, sposób ich realizacji komputerowej i przykładowe wyniki eksperymentów. Podane są również ćwiczenia symulacyjne i obliczeniowe oraz proste przykłady praktyczne z różnych dziedzin, np. fizyki, elektroniki, mechaniki.

Autorzy pragną serdecznie podziękować Panu prof. dr hab. inż. Zygmuntowi Hasiewiczowi, autorowi pierwszego zestawu ćwiczeń laboratoryjnych z Podstaw Automatyki, na bazie którego mogli rozwinąć i udoskonalić ich zakres tematyczny, wprowadzając jednocześnie komputerową implementację w środowisku MATLAB.

1.2. Istota i cele symulacji komputerowej

W celu podkreślenia znaczenia symulacji komputerowej rzeczywistych zjawisk dynamicznych omówiono kolejne fazy projektowania układu automatycznej regulacji na przykładzie sterowania poziomem wody w jeziorze. Pierwszym krokiem jest zdefiniowanie obiektu sterowania i ustalenie sygnału wyjściowego y(t) obiektu, jako celu sterowania, czyli takiej jego cechy fizycznej, którą należy sterować. Określa się również sygnał wejściowy u(t) - wielkość fizyczną mającą zasadniczy wpływ na y(t), np. obiekt - jezioro z zaporą na rzece, y(t) - poziom wody w jeziorze w chwili t, u(t) - położenie zasuwy w zaporze w chwili t.

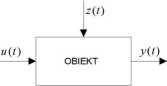
Rys. 1.1. Graficzna reprezentacja obiektu regulacji

Na obiekt oddziałują również inne wielkości z{t) - zwane zakłóceniami, trudne lub zbyt kosztowne w analizie, często o charakterze przypadkowym (np. opady deszczu, parowanie). Dla obiektu z rysunku 1.1 poszukuje się możliwie najlepszej formuły matematycznej T (wzoru, funkcjonału) opisującej zależność y{t) od u{t)

y(t) « J-{u{t — r)), gdzie r = 0,..., oo