1002889893

cos (beta)=—=

sin(be,a)=^Z^=

'Ix₂+y₂+z₂²

W kolejnych krokach wykonamy przekształcenie:

Krok 1: T(—X₀,—y₀,—Z₀) Krok 2: R.(-alfa) Krok 3: R_y{—beta)

Krok 4: R_x[fi) Krok 5: R_y(beta) Krok 6: R_:(alfa) Krok 7; T(x₀,y₀,Z₀)

R_y(beta)*P=

s	0	Zi	0
r		r			X
0	1	0	0	*	y
_Zl	0	s	0		z
		—			.
r		r			1
0	0	0	1

Podobnie możemy wyznaczać macierz: R_v(—beta), R.(alfa),R_z(—alfa)

Zatem przekształcenie (transformacja) obrotu wokół osi o kąt (fi) możemy zapisać jako:

R_y{fi)=T(-x₀,-y₀,-z₀)*R_z{-alfa)*R_y(-beta)*R_x(fi)*R_y(beta)*R_:(alfa)*T(x₀,y₀,z₀)

Wykład 7 - Symetrie

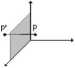
Symetrie wokół płaszczyzny (odbicia) Symetria względem płaszczyzny XY

		p		1	0	0	0
			x' = r	0	1	0	0
			y'=y	0	0	-1	0
		P'	z — z)	0	0	0	1

lewoskrętny (patrz -

Symetria ta zmienia również układ prawoskrętny przekształca układ współrzędnych).

Symetria.względem płaszczyzny YZ

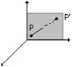
	-1	0	0	0
*'=—x)	0	1	0	0
y'=y \Symyz^=	0	0	1	0
z'=z J	0	0	0	1

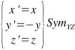
1	0	0	0
0	-1	0	0
0	0	1	0
0	0	0	1