12759 mat4

7. FUNKCJE TRYGONOMETRYCZNE

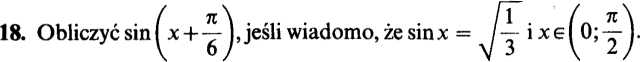
19.    Udowodnić, że jeżeli cos(x + y) = 0, to sin(x + 2y) = sinx.

20.    Sprowadzić do postaci iloczynowej:

a) sinx + cosx, d) sin²x — sin²y,

A) l+cosx,    e) 1— tg²x,

c) l+2sinx,    /) sin3x —sin2xcosx.

21. Sprowadzić do postaci iloczynowej:

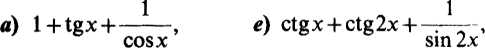
b) 1+sinx—cos2x,    /) cosx + cos2x + cos3x,

c) 2cos2x + sin2xtgx, g) sinx + sin3x + sin5x + sin7x.

d) sinx + tgx,

22. Sporządzić wykres funkcji:

a)    y = sin²x,

b)    y = (sin x + cos x)²,

c)    y = |sinx + cosx|,

/) y = |sin 4x + cos 4x|,

g)    y = |cos⁴x — sin⁴x|,

h)    y = |4sin³x — 3sinx|,

d)    y = sin²x—cos²x, ,■) y = ^3 sin2x-cos2x.

e)    y = 2 —3sin²x,

23.    Wykazać, że jeżeli <x + P + y = n, to

a)    sin2a + sin2/? + sin2y = 4 sina sin/?siny,

b)    sin²a + sin²/? + sin²y = 2 + 2cosacos/?cosy.

7t    TT

24.    Wykazać, że jeżeli a^—- + kn, keC i /? # — + ln, lei

Z    z

i y # y + m7r, meC i a + /? + y = 0, to tga + tg/? + tgy = tgatg/?tgy.

25.    Wykazać, że jeżeli a # kn, keC i /i ^ In, leC i y # mn, me i i a + /? + y = y, to ctga + ctg/? + ctgy = ctgactg/9ctgy.

----------ZADANIA 7.2

26.    Udowodnić, że sinx + sin0^ + x) + sin^+x) _{= 0}.

27.    Wykazać, że dla dowolnych x,yeS prawdziwa jest równość cos²x —sin²y = cos (x 4- y) cos (x —y).

' 2*- Udowodnić tożsamości:

. «) cos⁴X-sin⁴X = cos2x,

A) sin2x—tgx = cos2xtgx, c) 4sin⁴x + sin²2x = 4sin²x,

* d) 1 —tg²x =

cos2x

cos²x ’

^ COS X 4- ctg X .    .

' ’ ~«^r~^=1+sinx-

29. Udowodnić tożsamości:

1 £

sin 3x cos 3x

= 2,

smx cosx

^ ^ sinx 4- sin 3x + sin 5x 4- sin 7x

cos x 4-cos 3x4-cos 5x4-cos 7x 1 —sinx—cos2x + sin 3x sin 2x + 2 cos x cos 2x ^{= tgx}’ 2sin2x—sin4x 2sin2x+sin4x ^{= tg x}’

_ sin³x + sin3x r cos³x—cos3x ^{= Ctgx}’

1

^{= cos2x}-

•• Udowodnić tożsamości:

* tg3x —tg2x—tgx = tgxtg2x tg3x, sin2x cosx

= tg4x,

________

1 +cos2x l+cosx ^lg 2 ’

91