CCI00010
3
19. Wykazać, że jeżeli zdarżenia A i B są niezależne i ich suma jest zdarzeniem pewnym to albo P(A) = 1 albo P(B) = 1.
20. Pewna choroba występuje u 0,1 % ogółu ludności. Przygotowano test do jej wykrycia. Test ten daje wynik pozytywny u 97 % chorych i 1 % zdrowych. Obliczyć prawdopodobieństwo tego, że losowo wybrana osoba jest chora, jeśli test tej osoby dał wynik pozytywny.
21. Rzucamy trzy razy symetryczną monetą. Określmy zdarzenia: A - wypadnie przynajmniej jeden orzeł, B - wypadnie co najwyżej jedna reszka. Czy zdarzenia A i B są niezależne?
22. Rzucamy raz symetryczną kostkę do gry. Niech A oznacza zdarzenie -„wyrzucono parzystą liczbę oczek” oraz B - „wyrzucono liczbę oczek podzielną przez 3”. Czy zdarzenia A i B są niezależne?
23. Rzucamy dwa razy symetryczną kostkę do gry. Niech A oznacza zdarzenie
„ w pierwszym i drugim rzucie wypadła ta sama liczba oczek”, B zaś oznacza zdarzenie „w drugim rzucie wypadło co najmniej 5 oczek”. Czy zdarzenia A i B są niezależne?
24. Wiemy, że zdarzenia A, B i C są niezależne i każde z nich ma prawdopodobieństwo równe p. Obliczyć prawdopodobieństwo zdarzenia A^BuC.
25. Na 100 mężczyzn w wieku 40 do 60 lat 18 ma nadciśnienie tętnicze, zaś na 200 kobiet w tym samym wieku 11 ma nadciśnienie tętnicze. Z grupy o jednakowej liczbie kobiet i mężczyzn wylosowano osobę, która ma nadciśnienie.
a) Jakie jest prawdopodobieństwo, że jest to mężczyzna?
b) Jakie jest prawdopodobieństwo, że jest to kobieta?
26. Po upływie pewnego czasu T każda komórka może zginąć, przeżyć albo podzielić się na dwie odpowiednio z prawdopodobieństwem 1A, V* i Vz.
Jakie jest prawdopodobieństwo tego, że po upływie czasu 2T będą dwie komórki, gdy na początku była jedna?
ODPOWIEDZI:
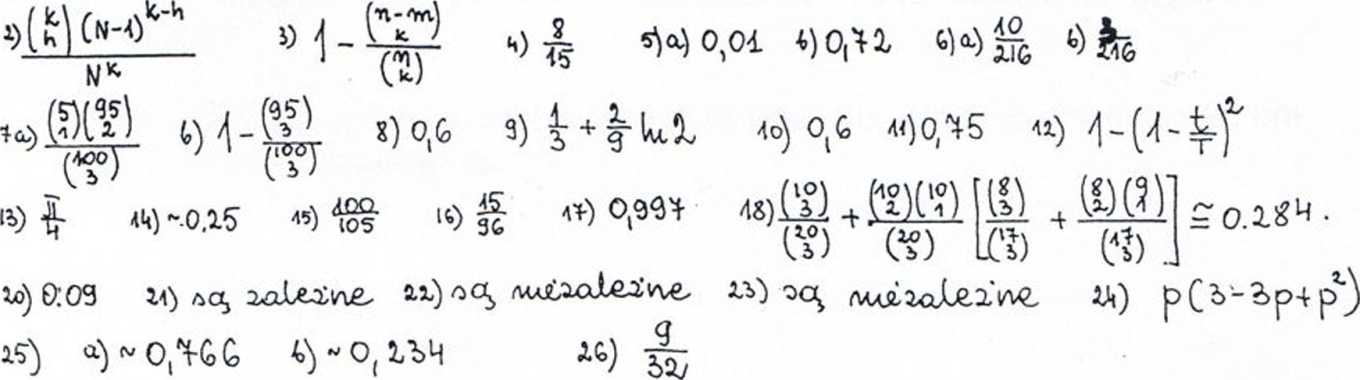
Wyszukiwarka
Podobne podstrony:
24 1. Zdarzenia i prawdopodobieństwo Twierdzenie 1.3.2. Jeżeli zdarzenia A i B są niezależne i Pr(B)
11092666D8280588663517?0312318 n 4. Zdarzenia A i B są niezależne. P(A)=0,2, a P(B)=0,5. Policz praw
img081 leż tym. że klasyfikacje nie są niezależne, to znaczy istnieje sprzężenie (interakcja) między
12759 mat4 7. FUNKCJE TRYGONOMETRYCZNE 19. Udowodnić, że jeżeli cos(x + y) = 0, to
od kandydatów przedstawienia uzasadnienia koniecznego do wykazania, że oferty te są poważne.
Powracając do modelu wicksellowskiego, podstawienie dP dl z równania (6) do (5) pozwala wykazać, że
1(20) W szczególności Einstein wykazał, że przestrzeń i czas są wzajemnie powiązane; oznacza to, że
Ekonomika turystyki R Łazarek (105) szych, miał to być pobyt u krewnych i znajomych. Sondaż wykaz
Image14 26 3.8. Wykazać, że jeśli zdarzenie B jest konsekwencją zdarzenia A,
Image14 (32) 26 3.8. Wykazać, że jeśli zdarzenie B jest konsekwencją zdarzenia A, to nie istnie
więcej podobnych podstron