Image14 (32)

26

3.8. Wykazać, że jeśli zdarzenie B jest konsekwencją zdarzenia A, to nie istnieje taki układ odniesienia, w którym zdarzenie B mogłoby zajść wcześniej niż A.

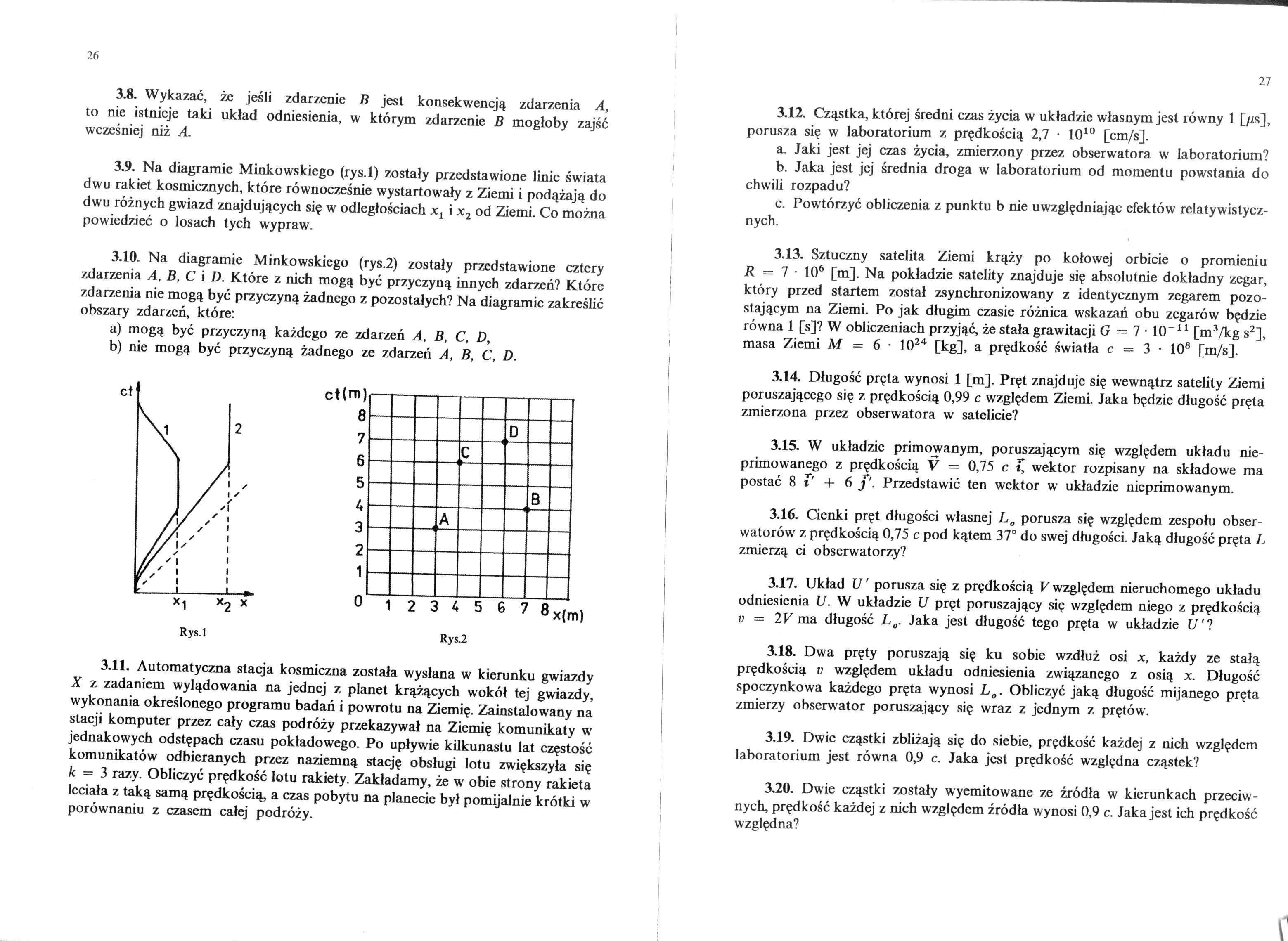
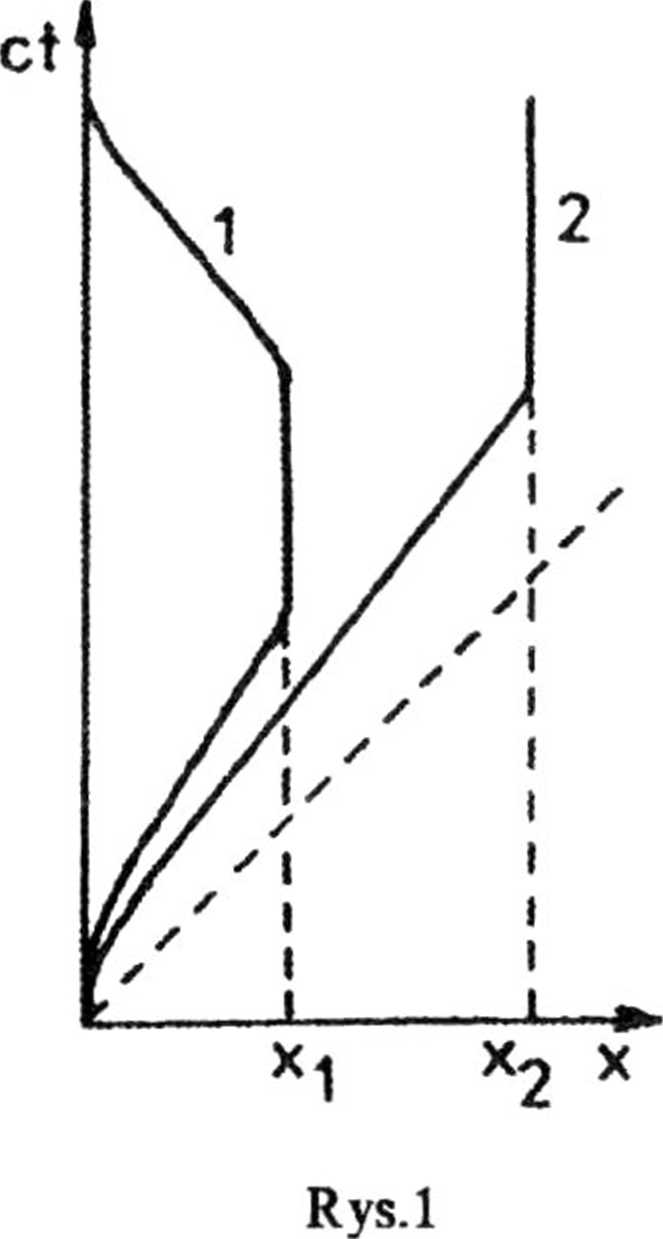
3.9. Na diagramie Minkowskiego (rys.l) zostały przedstawione linie świata dwu rakiet kosmicznych, które równocześnie wystartowały z Ziemi i podążają do dwu różnych gwiazd znajdujących się w odległościach x_L i x₂ od Ziemi. Co można powiedzieć o losach tych wypraw.

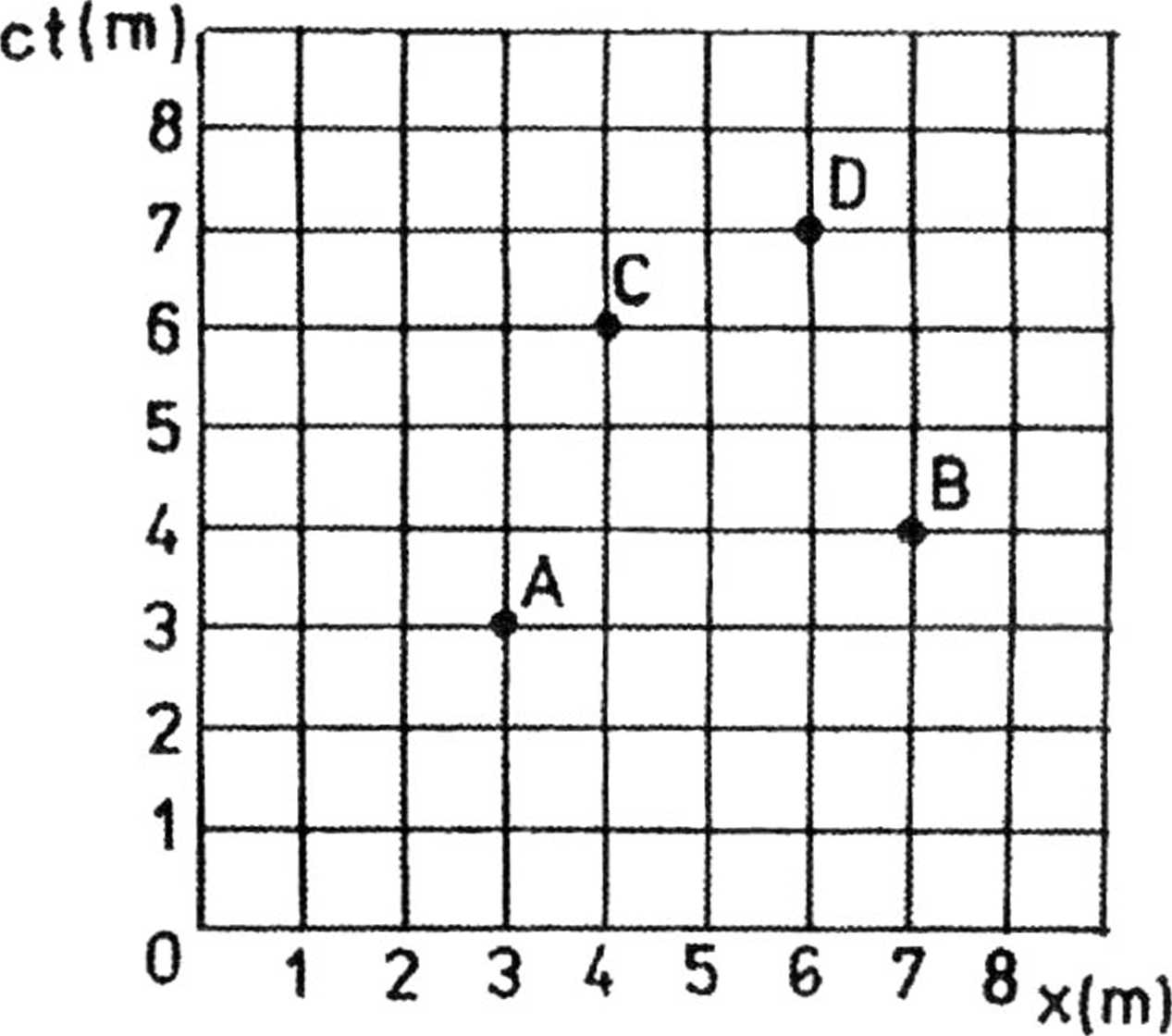
3.10. Na diagramie Minkowskiego (rys.2) zostały przedstawione cztery zdarzenia A, B, C i D. Które z nich mogą być przyczyną innych zdarzeń? Które zdarzenia nie mogą być przyczyną żadnego z pozostałych? Na diagramie zakreślić obszary zdarzeń, które:

a)    mogą być przyczyną każdego ze zdarzeń A, B, C, D,

b)    nie mogą być przyczyną żadnego ze zdarzeń A, B, C, D.

Rys.2

3.11. Automatyczna stacja kosmiczna została wysłana w kierunku gwiazdy X z zadaniem wylądowania na jednej z planet krążących wokół tej gwiazdy, wykonania określonego programu badań i powrotu na Ziemię. Zainstalowany na stacji komputer przez cały czas podróży przekazywał na Ziemię komunikaty w jednakowych odstępach czasu pokładowego. Po upływie kilkunastu lat częstość komunikatów odbieranych przez naziemną stację obsługi lotu zwiększyła się k = 3 razy. Obliczyć prędkość lotu rakiety. Zakładamy, że w obie strony rakieta leciała z taką samą prędkością, a czas pobytu na planecie był pomijalnie krótki w porównaniu z czasem całej podróży.

3.12. Cząstka, której średni czas życia w układzie własnym jest równy 1 [/is], porusza się w laboratorium z prędkością 2,7 • 10¹⁰ [cm/s].

a.    Jaki jest jej czas życia, zmierzony przez obserwatora w laboratorium?

b.    Jaka jest jej średnia droga w laboratorium od momentu powstania do chwili rozpadu?

c.    Powtórzyć obliczenia z punktu b nie uwzględniając efektów relatywistycznych.

3.13. Sztuczny satelita Ziemi krąży po kołowej orbicie o promieniu R = 7 • 10⁶ [m]. Na pokładzie satelity znajduje się absolutnie dokładny zegar, który przed startem został zsynchronizowany z identycznym zegarem pozostającym na Ziemi. Po jak długim czasie różnica wskazań obu zegarów będzie równa 1 [s]? W obliczeniach przyjąć, że stała grawitacji G = 7 • 10“¹¹ [m³/kg s²], masa Ziemi M = 6 • 10²⁴ [kg], a prędkość światła c = 3 • 10⁸ [m/s].

3.14. Długość pręta wynosi 1 [m]. Pręt znajduje się wewnątrz satelity Ziemi poruszającego się z prędkością 0,99 c względem Ziemi. Jaka będzie długość pręta zmierzona przez obserwatora w satelicie?

3.15.    W układzie primowanym, poruszającym się względem układu nie-primowanego z prędkością V = 0,75 c i, wektor rozpisany na składowe ma postać 8 i' + 6 j'. Przedstawić ten wektor w układzie nieprimowanym.

3.16.    Cienki pręt długości własnej L_a porusza się względem zespołu obserwatorów z prędkością 0,75 c pod kątem 37° do swej długości. Jaką długość pręta L zmierzą ci obserwatorzy?

3.17. Układ U' porusza się z prędkością V względem nieruchomego układu odniesienia U. W układzie U pręt poruszający się względem niego z prędkością v = 2V ma długość L_a. Jaka jest długość tego pręta w układzie U'l

3.18. Dwa pręty poruszają się ku sobie wzdłuż osi x, każdy ze stałą prędkością v względem układu odniesienia związanego z osią x. Długość spoczynkowa każdego pręta wynosi L₀. Obliczyć jaką długość mijanego pręta zmierzy obserwator poruszający się wraz z jednym z prętów.

3.19.    Dwie cząstki zbliżają się do siebie, prędkość każdej z nich względem laboratorium jest równa 0,9 c. Jaka jest prędkość względna cząstek?

3.20.    Dwie cząstki zostały wyemitowane ze źródła w kierunkach przeciwnych, prędkość każdej z nich względem źródła wynosi 0,9 c. Jaka jest ich prędkość względna?