1002889907

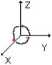
Kierunek patrzenia, dodatni obrót o 90 stopni X OY na OZ Y OZ na OX Z OX na OY

Wzory opisujące poszczególne przekształcenia w układzie prawoskrętnym łatwo przekształcić na wzory obowiązujące w układzie lewoskrętnym. Służą do tego przekształcenia układu współrzędnych, które punktu w drugim układzie.

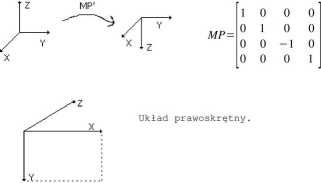
Translacje (przesuniecie)

Przesuniecie jest przekształceniem, które punktowi P(x,y,z) przyporządkowuje punkt P'(x',y',z'), gdzie

x' = x + tx y' = y + ty

gdzie tx,ty,tz są pewnymi liczbami rzeczywistymi. Mówimy też, że punkt P jest przekształceniem o wektor [tx,ty,tz]. Przekształcenie jako macierz przesunięcia będziemy oznaczać T(tx,ty,tz).

We współrzędnych jednorodnych mamy:

x'		1	0	0	tx		X		x+tx
y'	_	0	1	0	ty	*	y	_	y+ty
z'		0	0	-1	tz		z		z+tz
1		0	0	0	1		1		1

Skalownie wzaledem początku układu współrzędnych

punkt P(3	<,y,z>	na punkt P'(x	',y',z') taki, że
X'	= Sx	* X
y'	= Sy	* y
y'	= Sz	* z

Podobnie jak na płaszczyźnie w przestrzeni R³ obiekty mogą być zwiększane i zmniejszane w kierunku każdej z osi OX, OY, OZ. Ze współczynnikiem skalowania Sx, Sy, Sz odpowiednio. Skalowanie jest przekształceniem, które przeprowadza

gdzie Sx, Sy, Sz (wszystkie nierówne 0) są współczynnikami skalowania. Transformacje skalowania i macierz skalowania będziemy oznaczać przez S(Sx,Sy,Sz).

Macierz skalowania jest postaci: