1105139929

7

FUNDUSZ BUFFETTA BIJE AMERYKAŃSKĄ GIEŁDĘ

DANE W PROC.

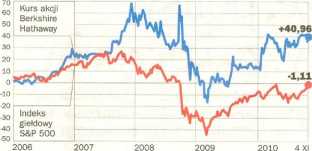
® GAZETA WYBORCZA    ŹRÓDŁO: GOOGLE RNANCE

Rysunek 1.1. Fundusz Warrena BufFetta versus indeks S&P500.

Tak więc wywodząca się od Markowitza analiza portfelowa nie jest jedyną strategią dostępną graczom giełdowym. Zostawiając teraz na boku wielkiego inwestora (który w pierwszych tygodniach obecnego kryzysu kupował jesienią 2008 za 8 miliardów dolarów akcje Goldman & Sachs i General Electric), wracajmy do idei, które upowszechnił Markowitz. Wprowadzimy mianowicie ideę opisu i mierzenia ryzyka przy kupnie akcji. W tym celu przyjrzyjmy się najpierw następującemu przykładowi.

Wyobraźmy sobie, że możemy zagrać w grę A, polegającą na tym, iż rzucamy raz symetryczną (uczciwą) monetą i jeśli wypadnie orzeł, to dostajemy złotówkę, natomiast jeśli wypadnie reszka, to my płacimy złotówkę. Jest to tzw. gra sprawiedliwa, gdyż szanse wygranej naszego rywala i nasze są równe (mówiąc nieco inaczej, średnia wygrana w tej grze jest równa zero). Każdy zapewne zgodziłby się po krótkim namyśle zagrać w taką grę - możemy się wzbogacić

0    złotówkę, a jeśli nawet przegramy, to nic szczególnie strasznego się nie stanie. Możemy więc uznać, że gra A jest mało ryzykowna.

Dość podobna jest gra B. Również rzucamy raz symetryczną monetą i jeśli wypadnie orzeł, to dostajemy 1000 zł, zaś jeśli wypadnie reszka, to płacimy 1000 zł. I ta gra jest sprawiedliwa - szanse wygranej są dla każdego z grających takie same. Widać jednak, że większość osób niechętnie zgodziłaby się zagrać w tę grę.

Zadajmy sobie więc pytanie, co różni obie te gry? Co sprawia, że jedna z nich wydaje się „niegroźna”, zaś w drugą zagralibyśmy już bardzo niechętnie? Bez wątpienia czujemy, że gra B niesie ze sobą dużo większe RYZYKO - możemy co prawda wiele zyskać, ale również bardzo dużo stracić. Jak jednak porównać ryzyka, wiążące się z tymi grami? Wyznaczmy najpierw średnie wygrane w każdej z gier.

Wygrana w grze A jest zmienną losową (oznaczmy ją przez X), przyjmującą dwie wartości:

1    z prawdopodobieństwem | (jest to szansa wyrzucenia orła w rzucie symetryczną monetą) oraz —1 (stratę rozumiemy, jako wygraną ujemną) również z prawdopodobieństwem \ (szansa wyrzucenia reszki). Zatem średnia wygrana w tej grze będzie wartością oczekiwaną zmiennej losowej, oznaczającej wygraną w grze A. Wynosi więc ona E(X) = \ • 1 + 3 • (—1) = 0. Analogicznie wyznaczamy średnią wygraną w grze B. Również wynosi ona 0. Widzimy stąd, że wielkość średniej wygranej nie rozróżnia w żaden sposób naszych gier (mówi ona tylko, że obie