1105140229

10

ROZDZIALI. RACHUNEK ZDAŃ

Zauważmy, że istnieją zdania, które są spełnialne, ale nie są tautologiami ani też zdaniami sprzecznymi.

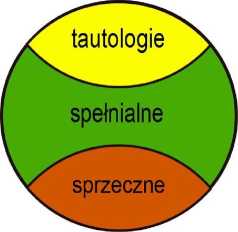
Przykładami tautologii są zdania po V -<po i T. Przykładami zdań spełnialnych, które nie są tautologiami sąpo, pi, po Vpi, po Api, po A (->pi). Przykładami zdań sprzecz-nych sąpoM^Po). ■!•

1.2 Przegląd Najważniejszych Tautologii

W rozdziale tym symbole p, q, r, s, t będą oznaczać dowolne zmienne zdaniowe. Rozważania rozpoczniemy od podstawowych własności koniunkcji oraz alternatywy. Zdania we wszystkich tabelkach zamieszczonych w tym rozdziale są tautologiami. Nie będziemy ich dowodzili. Pozostawiamy to czytelnikom jako proste ćwiczenie.

	Nazwa	Tautologia
1.	idempotentność	(p A p) <-> p
		(p V p) «-»■ p
2.	przemienność	(P A «)<->(? A p)
		(P V q) <-> (q V p)
3.	łączność	{p A (q A r)) -O- ((p Aq) Ar)
		(pV (qV r)) <-> ((p V q) V r)
4.	rozdzielność	(p A (q V r)) -f4 ((p A q) V (p A r)
		(p V {q A r)) ((p V q) A (p V r)

Przemienność jest własnością, którą czytelnik z pewnością zna w kontekście podstawowych działań arytmetycznych. Dodawanie i mnożenie liczb rzeczywistych są działaniami przemiennymi. Zwróćmy jednak uwagę na to, że potęgowanie liczb rzeczywistych nie jest operacją przemienną. Łączność jest własnością, którą również posiadają dodawanie i mnożenie liczb rzeczywistych. Jest to bardzo ciekawa własność, gdyż wynika z niej, że wynik działania nie zależy od pogrupowania pod-wyrażeń. W szczególności, możemy posługiwać się skrótem p A q A r, gdyż bez względu na to, jak w tym wyrażeniu rozłożymy nawiasy, to otrzymamy równoważne wyrażenie. Mnożenie liczb rzeczywistych jest rozdzielne względem dodawania, czyli x ■ (y + z) = x ■ y + x ■ z. Jednakże dodawanie liczb rzeczywistych nie jest rozdzielne względem mnożenia.