1954687383

ł jest równa ilości wymienionego w rozpatrywanej przemianie ciepła

/ 8Qv=coast = tiCv(Tb — Ta),

Ja

zaś wykonana praca to

r^B

/ <5WV=const = 0.

3.3.2. Przemiana izobaryczna

W tej przemianie pojemność cieplna n moli gazu doskonałego wynosi

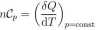
a praca 8W = pdV. Z I zasady termodynamiki nC_pdT = dU + pdV = nCydT + pdV.

Ponieważ pdV = nRdT (dlaczego?), to nCpdT — nCydT = nR d T, co prowadzi do wzoru Mayera (1814-1878)

C_p-C_v = R-    (18)

Ilość wymienionego w tej przemianie ciepła wynosi

J 8Q_P=const = uC_p(Tb — Ta),

wykonana praca

r 8W_p=const = Fpdv = p(V_B - V_A),

Ja    Ja

a całkowita zmiana energii wewnętrznej

F d£/_p=const = vC_v(Tb — Ta).

Ja

3.3.3. Przemiana izotermiczna

Temperatura gazu pozostaje stała, zatem

rB

/ dU_T=coast = 0,

Ja

tj. w tej przemianie U = const.

Zadanie 18. Uzasadnić ostatnią równość.

Z I zasady termodynamiki wynika więc, że 8W_T=const <^Qr=const-

Policzmy wartość pracy w przemianie izotermicznej:

r^B    r^vb dV    Vr    Vr

Wr_=Const — / pdV — const • /    — — const • ln— = nRT ln —.    (19)

Ja    Jva V    Va    Ka

gdzie const = nRT, co wynika z równania Clapeyrona (3).

Zadanie 19. Uzasadnić ostatnią równość.

Całkowita ilość ciepła Qt=const wymienionego w tej przemianie wynosi

Qt=const = Wr=const.    (20)

Na przykładzie tej przemiany możemy zrozumieć bliżej pojęcie przemiany kwazistacjonarnej. Gdybyśmy zbyt szybko poruszali tłokiem, pod którym znajduje się gaz, to ciśnienie wywierane przez gaz byłoby nieco mniejsze od ciśnienia wynikającego z równania izotermy. Zatem wykonana przez gaz praca byłaby mniejsza od pracy gazu wykonanej w warunkach równowagowych,

17