3093695799

E. I rój k ą t .p r o s t o. k ąt. n y

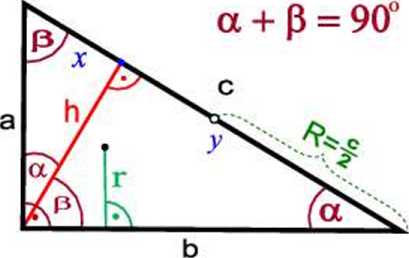
gdzie:

a. h - długości przyprostokątnych c - długość przeeiwprostokątnej a, /? - kąty ostre trójkąta prostokątnego ii - wysokość poprowadzona do boku c r - promień okręgu wpisanego w trójkąt R - promień okręgu opisanego na trójkącie

x, y - odcinki na jakie wysokość h podzieliła prz.eeiwprostokątną: c = x +y.

Trójkąt prostokątny - posiada jeden kąt prosty.

(1)    Suma kątów ostrych: a + p = 90°

(2)    Twierdzenie pitagorasa: a² + b² = c²

- suma kwadratów przyprostokątnych jest równa kwadratowi przeeiwprostokątnej.

(3)    Pole trójkąta:

a • b c • li c² • sin /? a² - tg/?

^Pi " ~T~ ~~2~    4    "    2

(4)    Promienie okręgów:

1    a + b - c

2    2 *

(5)    Wysokość i boki:

h = ^. li² = xy, a² = cx. b² = cy, a = c sin ct-c cos (3 = b tg a = b / tg (3 = y[cx

przyprostokątna

przyprostokątna

SINUS KĄTA a:    siiiff =

COSINUS KĄTA a    cos a =

TANGENS KĄTA a:    tga =

COTANGENS KĄTA a:    ctg a =

długość przy prostokątnej naprzeciw kąta a długość przed wprostok ątnej

długość przyprostokątnej przy kącie a dł ugość przeci wprostok ątnej

długość przyprostokątnej naprzeciw kąta a długość przyprostokątnej przy kącie a

długość przyprostokątnej przy kącie q długość przyprostokątnej naprzeciw kąta a

= cos/? = sili/?

= ctg/?

= tgp

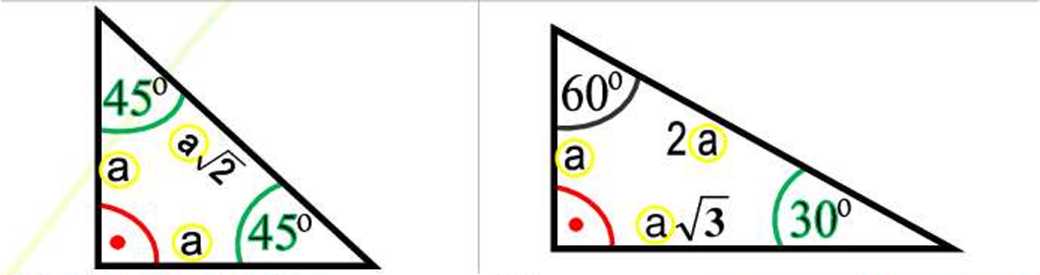
SZCZEGÓLNE PRZYPADKI TRÓJKĄTA PROSTOKĄTNEGO -podstawówka

trójkąt: 45°. 45°, 90°    trójkąt: 30°. 60°. 90°

© Copyright by Ewa Kędziorczyk

- 3(X) -

w w w. ma tematyka. sosu o wiec.p I