8299308009

Eksperymentalna weryfikacja sterowania programowego dźwignicy ... 169

w czasie jego współrzędne (punkt C₂ z rys. 1), r_d{t) — \x_d(t) z_d(t)]^T, a sterowanie realizowane jest przez siłę F sterującą położeniem wózka oraz moment M_w na bębnie wciągarki regulujący długość liny. Dynamiczne równania ruchu suwnicy laboratoryjnej mają postać [7]:

m, + m /w sin 6 - ^4J» x 2 m-\--f-	ml cos#	s		m <p{li cos 6 - W sin Ó)
	0	7	+	-ml 6^2
rv X X	ml^2	e		2 mlW

0

mg(cosd-1) - mgl sin 0

(i)

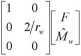
Równania (1) użyto do sformułowania równań ruchu programowego dźwignicy realizującej zadany ruch ładunku, opisanych w [3-6]. Rozwiązaniem tych równań (zadanie symulacji dynamicznej odwrotnej) są przebiegi w czasie zmiennych stanu dźwignicy w zadanym ruchu, w tym ą_d(t) = [s_d(t) l_d(t) 0_d(t)]⁷ oraz wymaganego sterowania dźwignicą, F_d(t) oraz    . Ze względów technicznych [7] zrezygnowano ze sterowania

suwnicą zgodnie z tymi wyliczonymi przebiegami nominalnymi (próby realizacji zadanych manewrów w ten sposób nie spełniły oczekiwań). Zamiast tego zastosowano sterowanie pozycją wózka i długością liny tak, by realizować ich żądane przebiegi, s_d(t) oraz l_d(t) . Było to sterowane w czasie rzeczywistym pod kontrolą programów Matlab oraz dSpace (czas próbkowania 5ms), z wykorzystaniem korektora proporcjonalnego (regulator P), który zapewnia nadążanie układu za narzuconymi s_d(t) oraz l_d(l). Korektor ten zapewnia również kompensację tarcia między belką a wózkiem suwnicy, nieuwzględnianego w modelu obliczeniowym. Konieczność takiej kompensacji tarcia wynika z silnie nieliniowej jego natury, trudnej do zamodelowania oraz identyfikacji.

3. WYNIKI BADAŃ LABORATORYJNYCH 3.1. Informacje ogólne

Na opisanym stanowisku laboratoryjnym przeprowadzono szereg eksperymentów dla różnych punktów początkowych i końcowych położenia ładunku. Wszystkie manewry były manewrami typu „rest-to-rest” (od spoczynku do spoczynku), co odpowiada rzeczywistemu cyklowi pracy dźwignicy. W niniejszej pracy zaprezentowano wyniki dla manewru, w którym ładunek przemieszczał się po torze krzywoliniowym, naszkicowanym wstępnie za pomocą sekwencji punktów, a następnie aproksymowanym za pomocą funkcji sklejanych trzeciego stopnia. Zadawany był następnie ruch ładunku wzdłuż tego toru, za pomocą odpowiednio gładkiej funkcji zmiany położenia na torze w czasie, spełniającej warunek manewru „rest-to-rest”. Zagadnienie to opisane jest szczegółowo w [6],

Czas symulacji badanego manewru wynosił r = 3s, a czasy faz rozruchu i hamowania wynosiły po r₀ =ls. Ruch ładunku odbywał się z punktu początkowego o współrzędnych 7^(0,-1.4) do punktu końcowego o współrzędnych 7^(1,-1.4) wzdłuż toru krzywoliniowego