1257951421

80

wariant d

s_n= 0,03

0,025

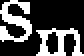
wykładnik pełzania n:    p,_n = 3_?

pozostałe dane jak wariant c

wariant e

wykładnik funkcji zniszczenia m:    p_m = 2,5,

pozostałe dane jak wariant d.

1.00000

03

CD

N

O

N

CO

N

O

co

<D

O

O

o

o

03

Cl

0.10000

0.01000

0.00100

0.00010

0:00001

0.00000

Rys. 6.9. Wpływ odchylenia standardowego wykładnika zniszczenia m na zmianę prawdopodobieństwa zniszczenia tarczy

1 - Sm = 0,0125, 2 - s_m = 0,025, 3 - s_m = 0,05

Fig. 6.9. Influence of exponent m standard deviations on the time variation of the pro-

bability of rotor — disc failure

1 - Sm = 0,0125, 2 - s_m = 0,025, 3 - s_m = 0,05

Rezultaty przedstawiono na rys. 6.8. Największy wpływ na prawdopodobieństwo zniszczenia wywiera wariancja wykładnika m. Wpływ wariancji wykładnika m na prawdopodobieństwo zniszczenia obrazuje szczegółowo rys. 6.9. Przedstawione tam rezultaty dotyczą obliczeń dla różnych wartości odchylenia standardowego wykładnika s_m przy założeniu deterministycznego charakteru pozostałych wielkości. Stosunkowo niewielki wpływ na prawdopodobieństwo zniszczenia ma wariancja gęstości materiału i wymiarów geometrycznych tarczy. Uzasadnione jest zatem traktowanie tych wielkości jako zdeterminowane.

—
—
—
—
									_
									[
									f

t / t_d

Rys. 6.10. Przebieg czasowy prawdopodobieństwa zniszczenia tarczy wirnikowej dla różnych wartości odchylenia standardowego granicznej wartości parametru zniszczenia coi ( 1 - so)i = 0,01; 2 - Stoi = 0,05; 3 - s_wl = 0,09)

Fig. 6.10. Time variation of the probability of rotor-disc failure for different standard

deviations of limiting value cdi (1 - Stoi = 0,01; 2 - Swi = 0,05; 3 - Scol = 0,09)